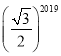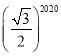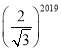题目内容
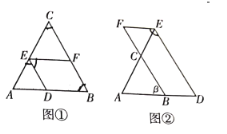
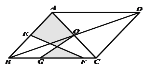
【题目】如图,在平行四边形ABCD中,对角线相交于点O,AC=AB, E是AB边的中点,G、F为 BC上的点,连接OG和EF,若AB=13, BC=10,GF=5,则图中阴影部分的面积为( )
A.48B.36C.30D.24
【答案】C
【解析】
连接EO,设EF,GO交于点H,过点H作NM⊥BC与M,交EO于N,过点A作AP⊥BC,将阴影部分分割为△AEO,△EHO,△GHF,分别求三个三角形的面积再相加即可.
解:如图连接EO,设EF,GO交于点H,过点H作NM⊥BC与M,交EO于N,
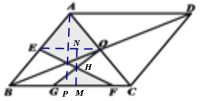
∵四边形ABCD为平行四边形,O为对角线交点,
∴O为AC中点,
又∵E为AB中点,
∴EO为三角形ABC的中位线,
∴EO∥BC,
∴MN⊥EO且MN=![]()
即EO=5,
∵AC=AB,
∴BP=PC![]() BC=5,
BC=5,
在Rt△APB中,![]() ,
,
∴三角形AEO的以EO为底的高为![]() AP=6,MN=
AP=6,MN=![]() =6
=6
∴![]() ,
,![]() ,
,
∴![]() ,
,
故选:C

练习册系列答案
相关题目