ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Οφ≤ΡΝœΘΚ
–ΓΟς”ωΒΫ’β―υ“ΜΗωΈ ΧβΘΚ
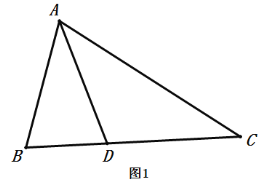
»γΆΦ1Θ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]() Θ°«σ÷ΛΘΚ
Θ°«σ÷ΛΘΚ![]()
–ΓΟςΆ®ΙΐΥΦΩΦΖΔœ÷Θ§Ω…“‘Ά®ΙΐΓΑΫΊ≥ΛΓΔ≤ΙΕΧΓ±ΝΫ÷÷ΖΫΖ®ΫβΨωΈ ΧβΘΚ
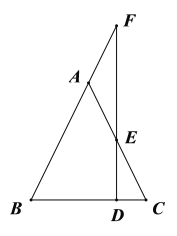
ΖΫΖ®1ΘΚ»γΆΦ2Θ§‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Ω…“‘ΒΟΒΫ»ΪΒ»»ΐΫ«–ΈΘ§ΫχΕχΫβΨωΈ Χβ
Θ§Ω…“‘ΒΟΒΫ»ΪΒ»»ΐΫ«–ΈΘ§ΫχΕχΫβΨωΈ Χβ
ΖΫΖ®ΕΰΘΚ»γΆΦ3Θ§―”≥Λ![]() ΒΫΒψ
ΒΫΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Ω…“‘ΒΟΒΫΒ»―ϋ»ΐΫ«–ΈΘ§ΫχΕχΫβΨωΈ Χβ
Θ§Ω…“‘ΒΟΒΫΒ»―ϋ»ΐΫ«–ΈΘ§ΫχΕχΫβΨωΈ Χβ
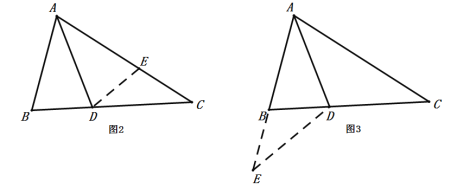
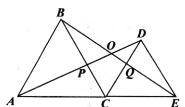
Θ®1Θ©ΗυΨί‘ΡΕΝ≤ΡΝœΘ§»Έ―Γ“Μ÷÷ΖΫΖ®÷ΛΟς![]()
Θ®2Θ©ΗυΨίΉ‘ΦΚΒΡΫβΧβΨ≠―ιΜρ≤ΈΩΦ–ΓΟςΒΡΖΫΖ®Θ§ΫβΨωœ¬ΟφΒΡΈ ΧβΘΚ»γΆΦ4Θ§ΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() «
«![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΧΫΨΩ
Θ§ΧΫΨΩ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟς
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟς
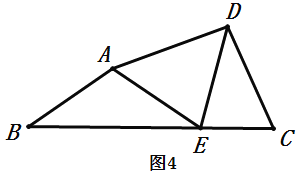
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©![]() Θ§÷ΛΟςΦϊΫβΈω
Θ§÷ΛΟςΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΖΫΖ®“ΜΘ§‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§”ΟSASΕ®άμ÷ΛΟς
Θ§”ΟSASΕ®άμ÷ΛΟς![]() Θ§»ΜΚσΒΟΒΫ
Θ§»ΜΚσΒΟΒΫ![]() Θ§
Θ§![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() Θ§»ΜΚσάϊ”ΟΒ»Ϋ«Ε‘Β»±Ώ«σ÷Λ
Θ§»ΜΚσάϊ”ΟΒ»Ϋ«Ε‘Β»±Ώ«σ÷Λ![]() Θ§ ΙΈ ΧβΒΟΫβΘΜ
Θ§ ΙΈ ΧβΒΟΫβΘΜ
ΖΫΖ®ΕΰΘ§―”≥Λ![]() ΒΫΒψ
ΒΫΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ ΒΟΒΫΓœABC=2ΓœEΘ§¥”ΕχΒΟΒΫΓœE=ΓœCΘ§άϊ”ΟAASΕ®άμ÷ΛΟςΓςAEDΓ’ΓςACDΘ§¥”Εχ«σΫβΘΜ
Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ ΒΟΒΫΓœABC=2ΓœEΘ§¥”ΕχΒΟΒΫΓœE=ΓœCΘ§άϊ”ΟAASΕ®άμ÷ΛΟςΓςAEDΓ’ΓςACDΘ§¥”Εχ«σΫβΘΜ
Θ®2Θ©‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ «σΒΟ
Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ «σΒΟ![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() Θ§άϊ”ΟSASΕ®άμ÷ΛΟς
Θ§άϊ”ΟSASΕ®άμ÷ΛΟς![]() Θ§»ΜΚσάϊ”Ο»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ «σΫβΘ°
Θ§»ΜΚσάϊ”Ο»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ «σΫβΘ°
ΫβΘΚΘ®1Θ©ΖΫΖ®“ΜΘΚ»γΆΦ2Θ§‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§

ΓΏ![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§
Γύ![]()
”÷ΓΏ![]() Θ§
Θ§![]()
Γύ![]()
Γύ![]() Θ§
Θ§![]()
ΓΏ![]()
Γύ![]()
Γύ![]()
Γύ![]()
Γύ![]()
ΖΫΖ®ΕΰΘΚ»γΆΦ3Θ§―”≥Λ![]() ΒΫΒψ
ΒΫΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§

ΓΏ![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§
Γύ![]()
ΓΏ![]()
ΓύΓœABC=2ΓœE
”÷ΓΏ![]()
ΓύΓœE=ΓœC
ΓΏAD=AD
ΓύΓςAEDΓ’ΓςACD
ΓύAC=AE=AB+BE=AB+BD
Θ®2Θ©‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]()

ΓΏ![]()
Γύ![]()
Γύ![]()
ΓΏ![]()
Γύ![]()
Γύ![]()
ΓΏ![]()
Γύ![]()
Γύ![]()
Γύ![]()
Γύ![]() ,
,![]()
ΓΏ![]()
Γύ![]()
Γύ![]()
Γύ![]()
Γύ![]() Θ°
Θ°

ΓΨΧβΡΩΓΩ÷–Ιζ“ΤΕ·Ρ≥ΧΉ≤ΆΆΤ≥ωΝΥ»γœ¬ΝΫ÷÷ΝςΝΩΦΤΖ―ΖΫ ΫΘΚ
‘¬ΉβΖ―/‘Σ | ΝςΝΩΖ―Θ®‘Σ/ | |
ΖΫ Ϋ“Μ | 8 | 1 |
ΖΫ ΫΕΰ | 28 | 0.5 |
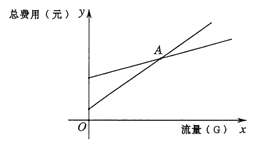
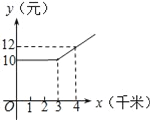
Θ®1Θ©…η“ΜΗω‘¬ΡΎ”Ο“ΤΕ·ΒγΜΑ Ι”ΟΝςΝΩΈΣ![]() Θ§ΖΫ Ϋ“ΜΉήΖ―”Ο
Θ§ΖΫ Ϋ“ΜΉήΖ―”Ο![]() ‘ΣΘ§ΖΫ ΫΕΰΉήΖ―”Ο
‘ΣΘ§ΖΫ ΫΕΰΉήΖ―”Ο![]() ‘ΣΘ®ΉήΖ―”Ο≤ΜΦΤΆ®ΜΑΖ―ΦΑΤδΥϋΖΰΈώΖ―Θ©Θ°–¥≥ω
‘ΣΘ®ΉήΖ―”Ο≤ΜΦΤΆ®ΜΑΖ―ΦΑΤδΥϋΖΰΈώΖ―Θ©Θ°–¥≥ω![]() ΚΆ
ΚΆ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ®≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩ
ΒΡΚ· ΐΙΊœΒ ΫΘ®≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈßΘ©ΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘ©ΘΜ
Θ®2Θ©»γΆΦΈΣ‘ΎΆ§“ΜΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Μ≠≥ωΘ®1Θ©÷–ΒΡΝΫΗωΚ· ΐΆΦœσΒΡ Ψ“βΆΦΘ§Φ«ΥϋΟ«ΒΡΫΜΒψΈΣΒψ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξΘ§≤ΔΫβ ΆΒψ
ΒΡΉχ±ξΘ§≤ΔΫβ ΆΒψ![]() Ήχ±ξΒΡ ΒΦ “β“εΘΜ
Ήχ±ξΒΡ ΒΦ “β“εΘΜ
Θ®3Θ©ΗυΨίΘ®2Θ©÷–Κ· ΐΆΦœσΘ§ΫαΚœΟΩ‘¬ Ι”ΟΒΡΝςΝΩ«ιΩωΘ§«κ÷±Ϋ”–¥≥ω―Γ‘ώΡΡ÷÷ΦΤΖ―ΖΫ ΫΗϋΚœΥψΘ°
ΓΨΧβΡΩΓΩΡ≥ΙΛ≥ßΉΦ±Η‘Ύ¥ΚΫΎ«Α…ζ≤ζΦΉΓΔ““ΝΫ÷÷–ΆΚ≈ΒΡ–¬ΡξάώΚ–Ι≤ 80 ΆρΧΉΘ§ΝΫ÷÷άώΚ–ΒΡ≥…±ΨΚΆ έΦέ»γœ¬±μΥυ ΨΘΜ
ΦΉ | ““ | |
≥…±ΨΘ®‘Σ/ΧΉΘ© | 25 | 28 |
έΦέΘ®‘Σ/ΧΉΘ© | 30 | 38 |
Θ®1Θ©ΗΟΙΛ≥ßΦΤΜ°≥οΉ Ϋπ 2150 Άρ‘ΣΘ§«“»Ϊ≤Ω”Ο”Ύ…ζ≤ζΦΉ““ΝΫ÷÷άώΚ–Θ§‘ρ’βΝΫ÷÷άώΚ–Ης…ζ≤ζΕύ…ΌΆρΧΉΘΩ
Θ®2Θ©Ψ≠Ιΐ –≥ΓΒς≤ιΘ§ΗΟ≥ßΨωΕ®‘Ύ‘≠ΦΤΜ°ΒΡΜυ¥Γ…œ‘ωΦ”…ζ≤ζΦΉ÷÷άώΚ–![]() ΆρΧΉΘ§‘ωΦ”…ζ≤ζ““÷÷άώΚ–
ΆρΧΉΘ§‘ωΦ”…ζ≤ζ““÷÷άώΚ–![]() ΆρΧΉΘ®
ΆρΧΉΘ®![]() Θ§
Θ§![]() ΕΦΈΣ’ΐ’ϊ ΐΘ©Θ§«“ΝΫ÷÷άώΚ– έΆξΚσΥυΜώΒΟΒΡΉήάϊ»σ«ΓΈΣ 690 Άρ‘ΣΘ§«κΈ ΗΟΙΛ≥ß”–ΦΗ÷÷…ζ≤ζΖΫΑΗΘΩ≤Δ–¥≥ωΥυ”–Ω…––ΒΡ…ζ≤ζΖΫΑΗΘ°
ΕΦΈΣ’ΐ’ϊ ΐΘ©Θ§«“ΝΫ÷÷άώΚ– έΆξΚσΥυΜώΒΟΒΡΉήάϊ»σ«ΓΈΣ 690 Άρ‘ΣΘ§«κΈ ΗΟΙΛ≥ß”–ΦΗ÷÷…ζ≤ζΖΫΑΗΘΩ≤Δ–¥≥ωΥυ”–Ω…––ΒΡ…ζ≤ζΖΫΑΗΘ°
Θ®3Θ©‘ΎΘ®2Θ©ΒΡ«ιΩωœ¬Θ§…η ΒΦ …ζ≤ζΒΡΝΫ÷÷άώΚ–ΒΡΉή≥…±ΨΈΣ![]() Άρ‘ΣΘ§«κ–¥≥ω
Άρ‘ΣΘ§«κ–¥≥ω![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΒ±
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΒ± ![]() ΈΣΕύ…Ό ±≥…±Ψ
ΈΣΕύ…Ό ±≥…±Ψ![]() ”–Ήν–Γ÷ΒΘ§≤Δ«σ≥ω≥…±Ψ
”–Ήν–Γ÷ΒΘ§≤Δ«σ≥ω≥…±Ψ![]() ΒΡΉν–Γ÷ΒΈΣΕύ…ΌΆρ‘ΣΘΩ
ΒΡΉν–Γ÷ΒΈΣΕύ…ΌΆρ‘ΣΘΩ