题目内容
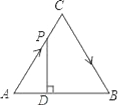
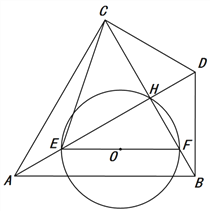
【题目】如图,等边三角形ABC中,AB=![]() ,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延
,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延
长线于点D,连结CD. 点E为线段AD上一点(不与点A,D重合),过点E作EF∥AB交BC于点
F,以EF为直径作⊙O. 设AE的长为![]() .
.
(1)求线段CD的长度.
(2)当点E在线段AH上时,用含x的代数式表示EF的长度.
(3) 当⊙O与四边形ABDC的一边所在直线相切时,求所有满足条件的![]() 的值.
的值.
【答案】(1)2;(2) ![]() ;(3)
;(3) ![]() 或
或![]() 或
或![]() ;
;
【解析】(1)根据等边三角形的性质可知,![]() 容易证明
容易证明![]() ≌
≌![]() ,
,![]()
(2)![]()
![]()
根据EF∥AB,![]() 即
即![]() 得到
得到![]() .
.
(3)分① 当⊙O与AC相切于点M时,②当⊙O与AB相切于点P时,③ 当⊙O与CD相切于点K时,三种情况进行讨论即可.
(1)根据等边三角形的性质可知,![]()
容易证明![]() ≌
≌![]() ,
,
![]()
(2)![]()
![]()
根据EF∥AB,
![]()
即![]()
得到![]() .
.
(3) ① 当⊙O与AC相切于点M时,如图①.

![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
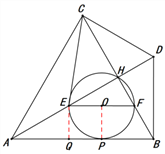
②当⊙O与AB相切于点P时,如图②.
![]()
![]() ,
,
![]() ,
, ![]() .
.
③ 当⊙O与CD相切于点K时,如图③.
连结HO.
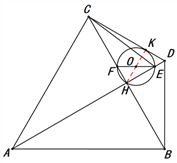
∵ ∠OHE+∠CDH=30°+60°=90°
∴ HO⊥CD
∵ OK⊥CD
∴ 点H,O,K三点共线.
![]() ,
,
![]() ,
,
综上所述,x的值为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目