题目内容
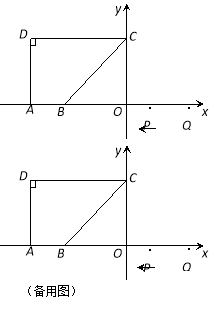
【题目】如图,抛物线![]() 交x轴于A,B两点(点A在点B的右侧),交y轴于点
交x轴于A,B两点(点A在点B的右侧),交y轴于点
C,顶点为D,对称轴分别交x轴、AC于点E、F,点P是射线DE上一动点,过点P作AC的平行线
MN交x轴于点H,交抛物线于点M,N(点M位于对称轴的左侧).设点P的纵坐标为t..
(1)求抛物线的对称轴及点A的坐标.
(2)当点P位于EF的中点时,求点M的坐标.
(3)① 点P在线段DE上运动时,当![]() 时,求t的值.
时,求t的值.
② 点Q是抛物线上一点,点P在整个运动过程中,满足以点C,P,M,Q为顶点的四边形是平行
四边形时,则此时t的值是 (请直接写出答案).

【答案】(1) (6,0);(2) M ![]() ;(3) ①
;(3) ①![]() ;
;
② ![]() 或
或![]() .
.
【解析】(1)根据对称轴公式即可直接求得对称轴方程,当y=0时,![]() ,解方程即可求出点A的坐标.
,解方程即可求出点A的坐标.
(2)求出点![]() 的坐标,求得直线方程
的坐标,求得直线方程![]() 联立方程即可求得点
联立方程即可求得点![]() 的坐标.
的坐标.
(3)①过点M作MK⊥x轴交于点K. 由MK//EF,![]() ,得
,得![]() MK=HK=3t,OK=3t-(2+t)=2t-2. 即M(2-2t,3t),列方程求解即可.
MK=HK=3t,OK=3t-(2+t)=2t-2. 即M(2-2t,3t),列方程求解即可.
②根据平行四边形的性质进行计算即可.
(1)对称轴直线x=![]() =2.
=2.
当y=0时,![]()
解得![]() .
.
所以对称轴为直线x=2,点A的坐标为(6,0).
(2)如图1,∵A(6,0),C(0,6)

∴OA=OC且∠AOC=90°
∵EF//y轴∴△AEF为等腰直角三角形
∴AE=EF=4若点P位于EF的中点,且MP//AC
则点H为AE的中点.
∴P(2,2),H(4,0)
∴![]()
则![]()
解得:![]() (舍去)
(舍去)
∴![]()
∴M ![]() .
.
(3)①如图2, 过点M作MK⊥x轴交于点K.
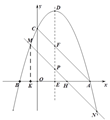
∵点P在线段DE上运动,则t > 0.
P(2,t),PE=EH=t.
由MK//EF,![]()
得:![]()
∴MK=HK=3t,OK=3t-(2+t)=2t-2.
即M(2-2t,3t)
![]() ,
,
化简:![]()
解得: ![]() (舍去)
(舍去)
∴点P在线段DE上运动时,当![]() 时, t的值为
时, t的值为![]()
② ![]() 或
或![]()

【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.