题目内容
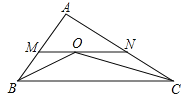
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
A. 7 B. 8 C. 9 D. 10
【答案】D
【解析】
利用角平分线及平行线性质,结合等腰三角形的判定得到MB=MO,NC=NO,将三角形AMN周长转化为AB+AC,求出即可.
∵BO为∠ABC的平分线,CO为∠ACB的平分线,∴∠ABO=∠CBO,∠ACO=∠BCO.
∵MN∥BC,∴∠MOB=∠OBC,∠NOC=∠BCO,∴∠ABO=∠MOB,∠NOC=∠ACO,∴MB=MO,NC=NO,∴MN=MO+NO=MB+NC.
∵AB=4,AC=6,∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10.
故答案为:10.

练习册系列答案
相关题目
【题目】某商场欲招聘一名员工,现有甲、乙两人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示:
应试者 | 计算机 | 语言 | 商品知识 |
甲 | 70 | 50 | 80 |
乙 | 60 | 60 | 80 |
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,计算两名应试者的平均成绩.从成绩看,应该录取谁?
(2)若商场需要招聘电脑收银员,计算机、语言和商品知识成绩分别占50%,30%,20%,计算两名应试者的平均成绩.从成绩看,应该录取谁?