题目内容
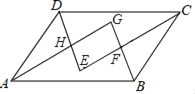
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC,BE=BC.当∠CBE:∠BCE=_________,求证:四边形ABCD是正方形.

【答案】2:3,证明见解析.
【解析】
首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,可得∠CDB=∠CBD,可得BC=CD,可得AD=BC,利用平行四边形的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形; 由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE =45°,可得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
证明:当∠CBE:∠BCE=![]() 时,四边形ABCD是正方形.
时,四边形ABCD是正方形.
理由如下:
在△ADE与△CDE中,
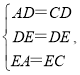
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
∵BE=BC
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∴∠CBE=180×![]() =45°,
=45°,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).