题目内容
【题目】如图，己如FG⊥AB，、CD⊥AB，垂足分别为G、D，∠1＝∠2．
求证：∠CED＋∠ACB＝180°请将下面的证明过程补充完整．
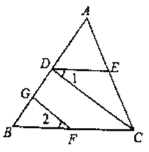
证明：∵FG⊥AB，CD⊥AB（已知），
∴∠FGB＝∠CDB＝90°(垂直的定义）
∴GF∥CD(___________________________)
∵GF∥CD(已证)
∴∠2＝∠BCD(___________________________)
又∵∠1＝∠2(已知)，
∴∠1＝∠BCD(___________________________)
∴___________________________，（___________________________)
∴∠CED＋∠ACB＝180°（___________________________)
【答案】同位角相等，两直线平行，两直线平行，同位角相等，等量代换，DE∥BC，内错角相等，两直线平行，两直线平行，同旁内角互补．
【解析】
根据同位角相等两直线平行证得GF∥CD，然后根据两直线平行同位角相等得出∠2=∠BCD，根据已知进一步得出∠1=∠BCD，即可证得DE∥BC，得出∠CED+∠ACB=180°．
证明：∵FG⊥AB，CD⊥AB（已知），
∴∠FGB＝∠CDB＝90°(垂直的定义）
∴GF∥CD(同位角相等，两直线平行)
∵GF∥CD(已证)
∴∠2＝∠BCD(两直线平行，同位角相等)
又∵∠1＝∠2(已知)，
∴∠1＝∠BCD(等量代换)
∴DE∥BC（ 内错角相等，两直线平行 ）
∴∠CED＋∠ACB＝180°（两直线平行，同旁内角互补)
故答案为：同位角相等，两直线平行，两直线平行，同位角相等，等量代换，DE∥BC，内错角相等，两直线平行，两直线平行，同旁内角互补．
名校联盟快乐课堂系列答案【题目】将长为20cm，宽为8cm的长方形白纸，按如图所示的方式粘合起来，粘合部分的宽为3cm．
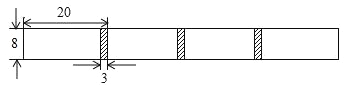
根据题意，将下面的表格补充完整：
白纸张数 | 1 | 2 | 3 | 4 | 5 |
|
纸条长度 | 20 | ______ | 54 | 71 | ______ |
|
直接写出用x表示y的关系式：______ ；
要使粘合后的总长度为1006cm，需用多少张这样的白纸？
【题目】将长为20cm，宽为8cm的长方形白纸，按如图所示的方式粘合起来，粘合部分的宽为3cm.
(1)根据题意，将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
（2）直接写出y与x的关系式.
(3）要使粘合后的长方形总面积为1656cm2，则需用多少张这样的白纸?
