题目内容
【题目】某校决定对初三学生进行体育成绩测试,成绩记入总分,同学们将根据自己平时的运动成绩确定自己的参考项目,下面是小亮同学的两个项目立定跳远和一分钟跳绳在近期连续五次测试的得分情况(立定跳远得分统计表和一分钟跳绳得分折线图):
立定跳远得分统计表
测试 日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
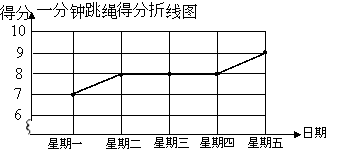
(1)请根据以上信息,分别将这两个项目的平均数、极差、方差填入下表:
统计量 | 平均数 | 极差 | 方差 |
立定跳远 | 8 | ||
一分钟跳绳 | 2 | 0.4 |
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的参考项目?请简述理由.
【答案】(1)填表见试题解析;(2)选一分钟跳绳理由见试题解析.
【解析】
试题分析:(1)先根据折线统计图得到一分钟跳绳的成绩为7、8、8、8、9;然后根据平均数、极差和方差的定义求解;(2)利用(1)中的计算结果得到平均分数相同,而一分钟跳绳成绩的极差和方差均小于立定跳远的极差和方差,说明一分钟跳绳的成绩较稳定,由此选一分钟跳绳.
试题解析:(1)
统计量 | 平均数 | 极差 | 方差 |
立定跳远 | 8 | 4 | 2 |
一分钟跳绳 | 8 | 2 | 0.4 |
(2)选一分钟跳绳,因为平均分数相同,但一分钟跳绳成绩的极差和方差均小于立定跳远的极差和方差,说明一分钟跳绳的成绩较稳定,所以选一分钟跳绳.
考点: ①统计初步;②极差、方差;③折线统计图.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).