题目内容
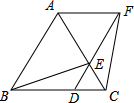
如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连结DE并延长至点F，使EF=AE，连结AF、BE和CF．
（1）请在图中找出一对全等三角形，并加以证明．
（2）判断四边形ABDF是怎样的四边形，并说明理由．
（3）若∠ABE=40°，求∠CFE的度数．
（1）请在图中找出一对全等三角形，并加以证明．
（2）判断四边形ABDF是怎样的四边形，并说明理由．
（3）若∠ABE=40°，求∠CFE的度数．
（1）证明：∵△ABC是等边三角形，
∴AC=BC=AB，∠ACB=60°；
又∵CD=CE，
∴△EDC是等边三角形，
∴DE=CD=CE，∠DCE=∠EDC=60°，
∵EF=AE，
∴EF+DE=AE+CE，
∴FD=AC=BC，
在△BCE和△FDC中，
，
∴△BCE≌△FDC（SAS）；
（2）四边形ABDF是平行四边形；
理由如下：
∵由（1）知△ABC、△AEF、△DCE均为等边三角形，
∴∠CDE=∠ABC=∠EFA=60°，
∴AB∥FD，BD∥AF，
∴四边形ABDF是平行四边形；
（3）∵△BCE≌△FDC，
∴∠EBC=∠CFD，
∵∠ABC=60°，∠ABE=40°，
∴∠CBE=∠CFE=20°．
∴AC=BC=AB，∠ACB=60°；
又∵CD=CE，
∴△EDC是等边三角形，
∴DE=CD=CE，∠DCE=∠EDC=60°，
∵EF=AE，
∴EF+DE=AE+CE，
∴FD=AC=BC，
在△BCE和△FDC中，
|
∴△BCE≌△FDC（SAS）；
（2）四边形ABDF是平行四边形；
理由如下：
∵由（1）知△ABC、△AEF、△DCE均为等边三角形，
∴∠CDE=∠ABC=∠EFA=60°，
∴AB∥FD，BD∥AF，
∴四边形ABDF是平行四边形；
（3）∵△BCE≌△FDC，
∴∠EBC=∠CFD，
∵∠ABC=60°，∠ABE=40°，
∴∠CBE=∠CFE=20°．
练习册系列答案
相关题目
