题目内容
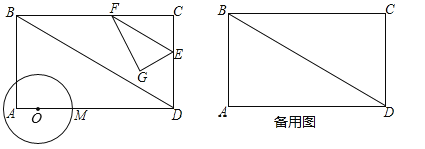
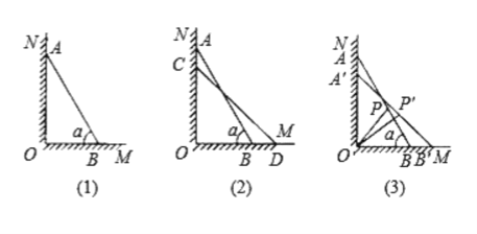
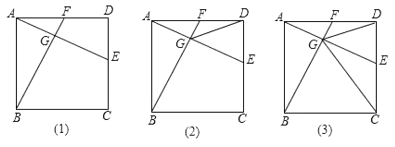
【题目】如图(1)在正方形![]() 中,点
中,点![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() ,重足为
,重足为![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() 平分
平分![]() ,如图(2),求证:点
,如图(2),求证:点![]() 是
是![]() 中点:
中点:
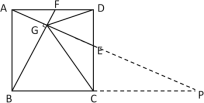
(3)在(2)的条件下,连接![]() ,如图(3),求证:
,如图(3),求证:![]() .
.
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)证明△BAF≌△ADE(ASA)即可解决问题;
(2) 过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,先根据AAS证得△BAG≌△AND,推出AG=DN,再由角平分线的性质可知DM=DN,即DM=AG,再证△AFG≌△DFM,推出AF=DF=DE=![]() AD=
AD=![]() CD,即点E是CD的中点 ;
CD,即点E是CD的中点 ;
(3)延长AE,BC交于点P,由(2)知DE=CD,证得△ADE≌△PCE,推出AE=PE,再根据中位线判定定理即可得到CB=PC,利用直角三角形斜边中线的性质可证明CG=![]() BP=BC=CP ,即为所证 .
BP=BC=CP ,即为所证 .
(1)证明:在正方形ABCD中,AB=AD,∠BAD=∠D=90o
∴∠2+∠3=90o
又 ∵ BF⊥AE ∴∠1+∠2=90o ∴∠1=∠3
在△BAF与△ADE中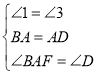
∴ △BAF≌△ADE
∴AF=DE

(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,
由(1)得∠1=∠3 , ∠BGA=∠AND=90o AB=AD
∴ △BAG≌△ADN ∴AG=DN
又DG平分∠EGF,DM⊥GF,DN⊥GE
∴ DM=DN
∴ DM=AG
又∠AFG=∠DFM , ∠AGF=∠DMF
∴ △AFG≌△DFM
∴AF=DF=DE=![]() AD=
AD=![]() CD
CD
即点E是CD的中点.
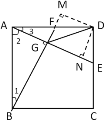
(3)延长AE,BC交于点P,由(2)知DE=CE,
∵∠ADE=∠ECP=90o,∠DEA=∠CEP
∴ △ADE≌△PCE
∴AE=PE
又∵CE∥AB ∴ BC=PC
在Rt△BGP中,BC=PC
∴CG=![]() BP=BC
BP=BC
∴CG=CD

【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数