题目内容
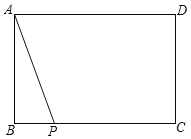
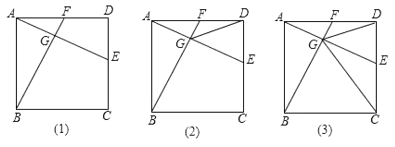
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
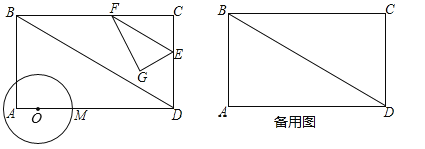
【答案】(1)a=2cm/s;(2)①t=![]() s或
s或![]() s时,直线FG与⊙O相切;②t=
s时,直线FG与⊙O相切;②t=![]() s时,点G在⊙O上.
s时,点G在⊙O上.
【解析】
(1)如图1中,当点G在AD上时,首先证明∠FEC=∠FEG=∠GED=60°,由EC=EG=![]() t,DE=
t,DE=![]() t,可得
t,可得![]() t+
t+![]() t=3
t=3![]() ,解方程即可;
,解方程即可;
(2)①如图2中,作GQ⊥AD于Q,GR⊥CD于R,QG的延长线交BC于P,FG的延长线交AD于T,解直角三角形求出TD,然后分情况讨论,分别列出方程求出相切时的时间;
②如图5中,作GN⊥AD,则DN=![]() t,ON=DN-OD=
t,ON=DN-OD=![]() t-(9-2t)=
t-(9-2t)=![]() t-9,NG=
t-9,NG=![]() ,OG=2,根据OG2=ON2+NG2,构建方程即可.
,OG=2,根据OG2=ON2+NG2,构建方程即可.
解:(1)如图1中,当点G在AD上时.
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=3![]() ,AD=9,
,AD=9,
∴tan∠BDA=![]() ,
,
∴∠ADB=30°,
∵BC∥AD,EF∥BD,
∴∠CFE=∠CBD=∠ADB=30°,
∴∠FEC=∠FEG=60°,
∴∠GED=60°,
∵CE=EG=![]() t,
t,
在Rt△GED中,DE=![]() t,
t,
∴![]() t+
t+![]() t=3
t=3![]() ,
,
∴t=2,
∴CE=EG=2![]() ,DE=
,DE=![]() ,DG=3,AG=6,
,DG=3,AG=6,
∵在整过移动过程中△EFG的直角顶点G能与点M重合,
∴2a+2=6,
∴a=2cm/s.
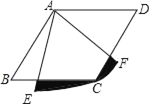
(2)①如图2中,作GQ⊥AD于Q,GR⊥CD于R,QG的延长线交BC于P,FG的延长线交AD于T.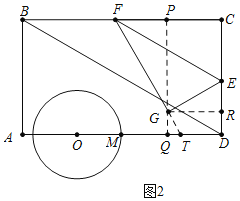
由题意CE=EG=![]() t,ER=
t,ER=![]() t,QD=PC=RG=
t,QD=PC=RG=![]() t,QG=DR=3
t,QG=DR=3![]() -
-![]() t-
t-![]() t=3
t=3![]() -
-![]() t,
t,
在Rt△GQT中,∵∠TGQ=30°,
∴QT=QGtan30°=3-![]() t,
t,
∴TD=![]() t-(3-
t-(3-![]() t)=3t-3,
t)=3t-3,
如图3中,当⊙O与FG相切于点N时,易知OA=2t,OT=![]() ,TD=3t-3,
,TD=3t-3,
则有2t+![]() +3t-3=9,
+3t-3=9,
解得t=![]() .
.
如图4中,当⊙O再次与FG相切时.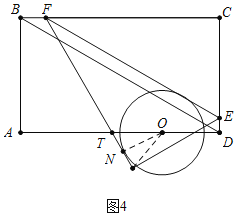
由OA+DT-OT=AD,可得2t+3t-3-![]() =9,
=9,
解得t=![]()
综上所述,t=![]() s或
s或![]() s时,直线FG与⊙O相切
s时,直线FG与⊙O相切
②如图5中,当点G在⊙O上时,
作GN⊥AD,则DN=![]() t,ON=DN-OD=
t,ON=DN-OD=![]() t-(9-2t)=
t-(9-2t)=![]() t-9,NG=
t-9,NG=![]() ,OG=2,
,OG=2,
∵OG2=ON2+NG2,
∴(![]() t-9)2+(
t-9)2+(![]() )2=4,
)2=4,
整理得:19t2-90t+104=0
∴(t-2)(19t-52)=0,
∴t=![]() 或t=2(舍弃)
或t=2(舍弃)
∴t=![]() s时,点G在⊙O上.
s时,点G在⊙O上.

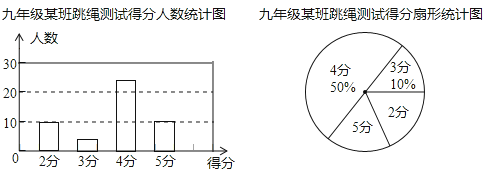
【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数 | 22 | 52 | 68 | 101 | 116 | 147 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.45 | 0.51 | 0.46 | 0.49 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).