题目内容
如图,⊙O的半径为6cm,射线PM与⊙O相切于点C,且PC=16cm.

(1)请你作出图中线段PC的垂直平分线EF,垂足为Q,并求出QO的长;
(2)在(1)的基础上画出射线QO,分别交⊙O于点A、B,将直线EF沿射线QM方向以5cm/s 的速度平移(平移过程中直线EF始终保持与PM垂直),设平移时间为t.当t为何值时,直线EF与⊙O相切?
(3)直接写出t为何值时,直线EF与⊙O无公共点?t为何值时,直线EF与⊙O有两个公共点?

(1)请你作出图中线段PC的垂直平分线EF,垂足为Q,并求出QO的长;
(2)在(1)的基础上画出射线QO,分别交⊙O于点A、B,将直线EF沿射线QM方向以5cm/s 的速度平移(平移过程中直线EF始终保持与PM垂直),设平移时间为t.当t为何值时,直线EF与⊙O相切?
(3)直接写出t为何值时,直线EF与⊙O无公共点?t为何值时,直线EF与⊙O有两个公共点?
解:(1)10;
(2)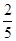 或
或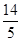 ;
;
(3)当0<t<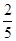 或t>
或t>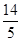 时,直线EF与⊙O无公共点,
时,直线EF与⊙O无公共点,
当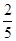 <t<
<t<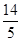 时,直线EF与⊙O有两个公共点.
时,直线EF与⊙O有两个公共点.
(2)
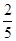 或
或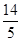 ;
;(3)当0<t<
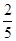 或t>
或t>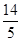 时,直线EF与⊙O无公共点,
时,直线EF与⊙O无公共点,当
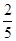 <t<
<t<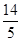 时,直线EF与⊙O有两个公共点.
时,直线EF与⊙O有两个公共点.分析:
(1)连接圆心和切点构造直角三角形,利用勾股定理求得QO的长;
(2)当直线EF与⊙O相切时,连接圆心与切点构造等边三角形求得直线EF运动的距离,除以速度即得到时间,本题应分内切和外切两种情况讨论;
(3)根据直线与圆相交和相离确定时间的取值范围。
解答:
(1)如图,连接OC,

∵PC切⊙O与点C,
∴OC⊥PC,
∵EF垂直平分PC,PC=16cm
∴QC=8cm,
∴QO2=QC2+OC2=100
∴QO=10厘米;
(2)当直线EF与⊙O相切于点D、交直线PM于点N时,连接OD.
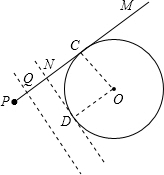
∴四边形ODNC是正方形,
∴CN=OD=6,
∴QN=QC+CN=6+8=14或QN=QC-CN=8-6=2,
∵直线EF沿射线QM方向以5cm/s 的速度平移,
∴t=2/5s或14/5s;
(3)当0<t<2/5或t>14/5时,直线EF与⊙O无公共点,
当2/5<t<14/5时,直线EF与⊙O有两个公共点。
点评:本题考查了勾股定理的应用、相似三角形的判定及性质及动点问题,解决动点问题的关键是化动为静。

练习册系列答案
相关题目
 .
.

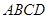 的边
的边 ,
,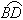 和
和 都是以
都是以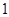 为半径的圆弧,则无阴影
为半径的圆弧,则无阴影


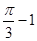

 内接于
内接于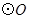 ,若
,若 ,则
,则 的大小为 ( )
的大小为 ( )

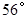


 ,半径为6,则扇形的弧长为 .(结果保留
,半径为6,则扇形的弧长为 .(结果保留 )
) 

 ,那么∠A的度数为
,那么∠A的度数为