题目内容
（11·永州）（本题满分10分）如图，AB是半圆O的直径，点C是⊙O上一点
（不与A，B重合），连接AC，BC，过点O作OD∥AC交BC于点D，在OD的延长线上
取一点E，连接EB，使∠OEB=∠ABC．
⑴ 求证：BE是⊙O的切线；
⑵ 若OA=10，BC=16，求BE的长．
（不与A，B重合），连接AC，BC，过点O作OD∥AC交BC于点D，在OD的延长线上
取一点E，连接EB，使∠OEB=∠ABC．
⑴ 求证：BE是⊙O的切线；
⑵ 若OA=10，BC=16，求BE的长．
证明：⑴∵AB是半圆O的直径 ∴∠ACB=90°
∵OD∥AC ∴∠ODB="∠ACB=90°" ∴∠BOD+∠ABC=90°
又∵∠OEB="∠ABC " ∴∠BOD+∠OEB="90° " ∴∠OBE=90°
∵AB是半圆O的直径 ∴BE是⊙O的切线
⑵在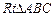
中，AB=2OA=20，BC=16，∴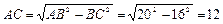
∴
∴
∴
．
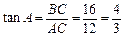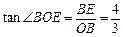
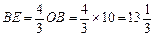∵OD∥AC ∴∠ODB="∠ACB=90°" ∴∠BOD+∠ABC=90°
又∵∠OEB="∠ABC " ∴∠BOD+∠OEB="90° " ∴∠OBE=90°
∵AB是半圆O的直径 ∴BE是⊙O的切线
⑵在
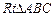中，AB=2OA=20，BC=16，∴∴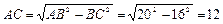
∴∴
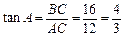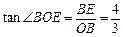
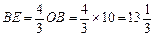．略
练习册系列答案
名校课堂系列答案
相关题目
的圆形纸片折叠后，圆弧恰好经过圆心
，则折痕
的
．
图，AB是⊙O的直径，点C，D都在⊙O上，连接CA，CB，DC，DB．已知∠D=30°，BC=3，则AB的长是 ．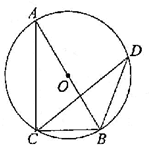
OC的度数；
得到△AED，AE交半圆于点F，连接DF。
