Question

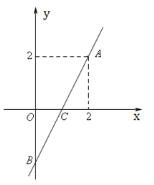
【题目】如图, 平面直角坐标系中，过点C（28，28）分别作x轴、y轴的垂线，垂足分别为B、A，一次函数y=x+3的图像分别与x轴和CB交于点D、E，点P 是DE中点，连接AP.

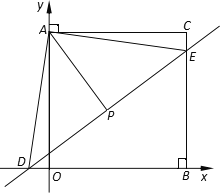
⑴ 求点D与点E的坐标； ⑵求证：△ADO≌△AEC；⑶ 求AP的长．

Answer 1

【答案】⑴点D（-4，0）；点E（28，24）；⑵ 见解析.⑶AP=20.

【解析】

（1）根据题意可求出E点横坐标为28，然后根据一次函数解析式即可求出D、E两点坐标；

（2）根据坐标即可求出OD=CE，然后根据题意即可证出四边形AOBC是正方形，从而得出AO =AC，∠AOD=∠C=90°，再利用SAS即可证出△ADO≌△AEC；

（3）根据全等三角形的性质可得：∠OAD=∠CAE，AD=AE，从而证出△ADE为等腰直角三角形，即可得到AP=DE，然后利用勾股定理即可求出DE，从而求出AP.

解：（1）∵CE垂直x轴，点C（28，28）

∴E点横坐标为28

∵一次函数y=x+3的图像分别与x轴和CB交于点D、E

当y=0时，解得：x=-4，当x=28时，解得：y=24

∴点D的坐标为（-4，0），点E的坐标为（28，24）

（2）∵点D的坐标为（-4，0），点E的坐标为（28，24），点C（28，28）

∴OD=4，CE=28－24=4

∴OD=CE

∵过点C（28，28）分别作x轴、y轴的垂线，垂足分别为B、A，

∴四边形AOBC是正方形

∴AO =AC，∠AOD=∠C=90°，点B的坐标为（28,0）

在△ADO和△AEC中

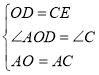
∴△ADO≌△AEC

（3）∵△ADO≌△AEC

∴∠OAD=∠CAE，AD=AE

∴∠OAD＋∠OAE=∠CAE＋∠OAE

∴∠DAE=∠OAC=90°

∴△ADE为等腰直角三角形

∵点P 是DE中点

∴AP=DE

∵点B的坐标为（28,0），点D（-4，0），点E（28，24）

∴BD=28－（-4）=32，BE=24－0=24

根据勾股定理：DE=

∴AP=DE=20