ЬтФПФкШн
ЁОЬтФПЁПЭМЂйЪЧвЛИіГЄЮЊ2mЃЌПэЮЊ2nЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљдШЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓАДЭМЂкаЮзДЦДГЩвЛИіе§ЗНаЮЃЎ

ЃЈ1ЃЉЧыгУСНжжВЛЭЌЗНЗЈЃЌЧѓЂкжавѕгАВПЗжЕФУцЛ§ЃЈВЛгУЛЏМђЃЉ
ЗНЗЈ1ЃКЁЁ ЁЁЃЛЗНЗЈ2ЃКЁЁ ЁЁЃЛ
ЃЈ2ЃЉЙлВьЭМЂкЃЌаДГіЃЈm+nЃЉ2ЃЌЃЈmЉnЃЉ2ЃЌmnжЎМфЕФЕШСПЙиЯЕ ЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЬтжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃК
ЂйШєa+bЃН7ЃЌabЃН5ЃЌЧѓЃЈaЉbЃЉ2ЕФжЕЃЛ
ЂкШє2a+bЃН5ЃЌabЃН2ЃЌЧѓ2aЉbЕФжЕЃЎ
ЁОД№АИЁП(1) ЃЈm+nЃЉ2Љ4mmЃЌЃЈmЉnЃЉ2ЃЛ(2) m2+2mn+n2Љ4mnЃНm2Љ2mn+n2ЃНЃЈmЉnЃЉ2;(3) Ђй29; ЂкЁР3
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвбжЊЭМаЮНсКЯБпГЄЮЊЃЈm+nЃЉЕФДѓе§ЗНаЮЕФУцЛ§МѕШЅГЄЮЊmЃЌПэЮЊnЕФ4ИіГЄЗНаЮУцЛ§вдМАБпГЄЮЊЃЈm-nЃЉЕФе§ЗНаЮЕФУцЛ§ЃЌЗжБ№ЧѓГіД№АИЃЛ
ЃЈ2ЃЉЗжБ№ЛЏМђЃЈ1ЃЉжаЧѓЕУвѕгАВПЗжЕФУцЛ§ПЩЕУД№АИЃЛ
ЃЈ3ЃЉЂйЂкРћгУЃЈ2ЃЉжаЙиЯЕЪНЃЌНЋвбжЊБфаЮЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉЗНЗЈ1ЃКЃЈm+nЃЉ2Љ4mnЃЌ
ЗНЗЈ2ЃКЃЈmЉnЃЉ2ЃЛ
ЙЪД№АИЮЊЃКЃЈm+nЃЉ2Љ4mnЃЛЃЈmЉnЃЉ2ЃЛ
ЃЈ2ЃЉЃЈm+nЃЉ2Љ4mnЃНЃЈmЉnЃЉ2
жЄУїЃКзѓБпЃНm2+2mn+n2Љ4mn
ЃНm2Љ2mn+n2
ЃНЃЈmЉnЃЉ2ЃНгвБпЃЛ
ЃЈ3ЃЉЂйЃЈaЉbЃЉ2ЃНЃЈa+bЃЉ2Љ4ab
ЃН72Љ4ЁС5
ЃН49Љ20=29ЃЛ
ЂкЃЈ2aЉbЃЉ2ЃНЃЈ2a+bЃЉ2Љ8ab
ЃН52Љ8ЁС2
ЃН25Љ16=9ЃЛ
Ёр2aЉbЃНЁР3ЃЛ

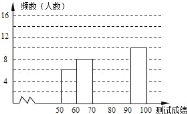
ЁОЬтФПЁПЁАЩЭжаЛЊЪЋДЪЃЌбАЮФЛЏЛљвђЃЌЦЗЩњЛюжЎУРЁБЃЌФГаЃОйАьСЫЪзНьЁАжаЙњЪЋДЪДѓЛсЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБФЌаД50ЪзЙХЪЋДЪЃЌШєУПе§ШЗФЌаДГівЛЪзЙХЪЋДЪЕУ2ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
ЃЈ1ЃЉЂйЦЕЪ§ЗжВМБэжаaЕФжЕЮЊЃЛЂкШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЃЛЂлНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЕк5зщ10УћЭЌбЇжаЃЌга4УћФаЭЌбЇЃЈгУAЃЌBЃЌCЃЌDБэЪОЃЉЃЌЯжНЋет4УћЭЌбЇЗжГЩСНзщЃЈУПзщ2ШЫЃЉНјааЖдПЙСЗЯАЃЌЧѓAгыBСНУћФаЭЌбЇФмЗждкЭЌвЛзщЕФИХТЪЃЎ
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 50ЁмxЃМ60 | 6 |
Ек2зщ | 60ЁмxЃМ70 | 8 |
Ек3зщ | 70ЁмxЃМ80 | 14 |
Ек4зщ | 80ЁмxЃМ90 | a |
Ек5зщ | 90ЁмxЃМ100 | 10 |