题目内容
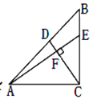
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.

【答案】证明见解析.
【解析】试题分析:要证明BC2=BG·BF即要证明△BCG∽△BFC,已知∠GBC=∠CBF,即要证明∠BCG=∠F,由于∠F=∠A,即要证明∠A=∠BCG,由已知条件不难证明.
试题解析:
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB于点D,
∴∠ACD+∠A=90°,
∴∠BCD=∠A.
又∵∠A=∠F,
∴∠F=∠BCD=∠BCG.
在△BCG和△BFC中,
∵![]() ,
,
∴△BCG∽△BFC.
∴![]() =
=![]() ,
,
即BC2=BG·BF.

练习册系列答案
相关题目