题目内容
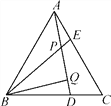
【题目】如图，等边△ABC中，AE＝CD，AD，BE相交于点P，BQ⊥AD于点Q.
(1)求证：BP＝2PQ；
(2)若PE＝1，PQ＝3，试求AD的长．
【答案】（1）见解析；（2）7
【解析】试题分析：
根据全等三角形的判定方法SAS可证得△BEC≌△ADB，根据各角的关系及三角形内角、外角和定理可证得
，即可得结论．
由已知条件，先证明△ABE≌△CAD得，可得
．即可求出
的长．
试题解析：
AE=CD，AC=BC，
∴EC=BD；
∵△ABC为等边三角形，
在△BEC与△ADB中，
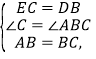
∴△BEC≌△ADB(SAS)，
∴∠EBC=∠BAD；
∵∠ABE+∠EBC=
,则∠ABE+∠BAD=，
∵∠BPQ是△ABP外角，
∴∠ABP+∠BAP==∠BPQ，
又∵BQ⊥AD，
∴BP=2PQ.
∵△ABC为等边三角形，
∴AB=CA，∠BAE=∠ACD=；
又∵AE=CD，
在△ABE和△CAD中，
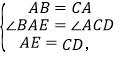
∴△ABE≌△CAD(SAS)；
∴BE=AD，∠CAD=∠ABE；
∵BQ⊥AD，
，则
∵PQ=3，
∴在Rt△BPQ中，BP=2PQ=6；
又∵PE=1，
∴AD=BE=BP+PE=7.
练习册系列答案
相关题目
【题目】某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）
备用体育用品 | 篮球 | 排球 | 羽毛球拍 |
单位（元） | 50 | 40 | 25 |
（1）若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？
（2）若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？若能，求出篮球、排球、羽毛球拍各购买多少件；若不能，请说明理由．
