题目内容
如图,在直角坐标系xOy中,已知菱形OABC的顶点O在坐标原点,顶点B在y轴正半轴上,OA边在直线y=![]() x上,AB边在直线y=-
x上,AB边在直线y=-![]() x+
x+![]() 上.
上.

(1)根据题意,直接写出菱形顶点,O、A、B、C的坐标,以及边长和∠AOC的度数;
(2)在OB上有一动点P,以O为圆心,OP为半径画弧MN,分别交OA、OC于点M、N(M、N可以与A、C重合),作⊙Q与AB、BC、弧MN都相切.设⊙Q的半径为R,OP的长为y,求y与R之间的函数关系式;
(3)以O为圆心,OA为半径作扇形OAC,请问在菱形OABC中,除去扇形OAC后的剩余部分内,是否可以作出一个圆,使所得的圆是以扇形OAC为侧面的圆锥的底面,若存在,求出这个圆的面积;若不存在说明理由.
答案:
解析:
解析:
|
(1)O、A、B、C坐标依次为(0,0),( ∠AOC=60°……………………………………(5分) ∴AO= (2)设⊙Q与AB相切于D连接QD,则QD=QP=R………………(7分) 又QD⊥AB,∠ABQ=30° ∴BQ=2R,∴OB=OP+PQ-BQ=y+R+2R……………………(9分) 即 (3)∵OA=1,∠AOC=60° ∴弧AC的长为 而此时⊙Q的半径 设⊙M符合条件,其半径为r,则⊙M周长=弧AC的长= ∴ ∵ 故能作一个圆,使这个圆是扇形OAC为侧面的圆锥的底面,它的面积为: |

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.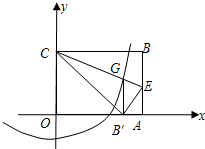 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.