��Ŀ����
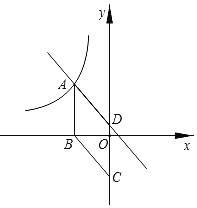
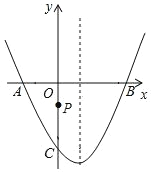
����Ŀ����ͼ����ֱ֪��![]() ��x�Ḻ�����ڵ�A����y���ڵ�C��������
��x�Ḻ�����ڵ�A����y���ڵ�C��������![]() ������A��C����x�����һ����ΪB��
������A��C����x�����һ����ΪB��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ������������һ����P�ĺ�����Ϊm��
������������һ����P�ĺ�����Ϊm��
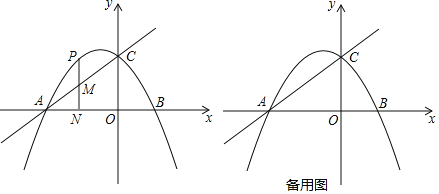
������P�ڵڶ��������������˶�����P��![]() ���ڵ�N��ֱ��AC�ڵ�M����ֱ��AC���߶�PN�ֳ�2��3������ʱ����m��ֵ��
���ڵ�N��ֱ��AC�ڵ�M����ֱ��AC���߶�PN�ֳ�2��3������ʱ����m��ֵ��
������CP���Ե�PΪֱ�Ƕ���������ֱ��������CPQ������Q���������ߵĶԳ�����ʱ����ֱ��д����P�����꣮
���𰸡�(1)![]() ��(1)��
��(1)��![]() ��
��![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]()
��������
��1������ֱ��![]() �������ύ�ڵ�A����C�������A����C���������κ�������ʽ���������
�������ύ�ڵ�A����C�������A����C���������κ�������ʽ���������
��2������P�����꣬��ʾ��PM��MN������ֱ��AC���߶�PN�ֳ�2��3�����֣����������������⼴�ɣ�
�ڸ��ݡ�CPQ�ǵ��������Σ���![]() ��
��![]() ����
����![]() ����P�����꣬��ʾ����K����G�����꣬����
����P�����꣬��ʾ����K����G�����꣬����![]() �������̽�����⼴�ɣ�
�������̽�����⼴�ɣ�
��1����![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() �����
�����![]() ����
����![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() �����
�����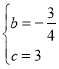 ��
��
![]() �����߽���ʽΪ
�����߽���ʽΪ![]() ��
��
��2������![]() ����
����![]() ��
��
![]() ��
��![]() ��
��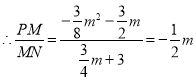 ��
��
![]() ֱ��AC���߶�PN�ֳ�2��3�����֣�
ֱ��AC���߶�PN�ֳ�2��3�����֣�
![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
![]() ��
��![]() ����G���������ߵĶԳ�����K����ͼ��
����G���������ߵĶԳ�����K����ͼ��
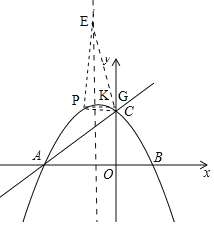
����ֱ��������CPQ��![]() ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() �������ߵĶԳ���Ϊֱ��
�������ߵĶԳ���Ϊֱ��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ���ⷽ��
���ⷽ��![]() ��
��![]() ��
��![]() ��
��
�ⷽ��![]() ��
��![]() ��
��![]() ��
��
![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��