Question

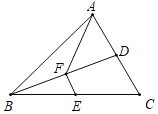
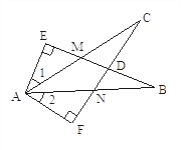
【题目】如图，EB交AC于M，交FC于D，AB交FC于N，∠E＝∠F＝90，∠B＝∠C，AE＝AF，给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN。其中正确的结论有（　）

A. 4个 B. 3个 C. 2个 D. 1个

Answer 1

【答案】B

【解析】∠E=∠F=90°，∠B=∠C，AE=AF可得△ABE≌△ACF，三角形全等的性质BE=CF；∠BAE=∠CAF可得①∠1=∠2；由ASA可得△ACN≌△ABM．④CD=DN不成立．

∵∠E=∠F=90°，∠B=∠C，AE=AF

∴△ABE≌△ACF

∴BE=CF

∠BAE=∠CAF

∠BAE-∠BAC=∠CAF-∠BAC

∴∠1=∠2

△ABE≌△ACF

∴∠B=∠C，AB=AC

又∠BAC=∠CAB

△ACN≌△ABM．

④CD=DN不能证明成立，3个结论对．

故选B．