题目内容
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F . 过点E作EG∥BC , 交AB于G , 则图中相似三角形有( ) 
A.4对
B.5对
C.6对
D.7对
【答案】B
【解析】解答:图中相似三角形有△ABC∽△CDA , △AGE∽△ABC , △AFE∽△CBE , △BGE∽△BAF , △AGE∽△CDA共5对, 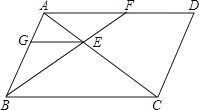
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC ,
∴△ABC≌△CDA , 即△ABC∽△CDA ,
∵GE∥BC ,
∴△AGE∽△ABC∽△CDA ,
∵GE∥BC , AD∥BC ,
∴GE∥AD ,
∴△BGE∽△BAF ,
∵AD∥BC ,
∴△AFE∽△CBE .
故选B .
分析:根据平行四边形的性质得出AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC , 推出△ABC≌△CDA , 即可推出△ABC∽△CDA , 根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目