题目内容
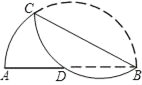
【题目】阅读下面材料:小明遇到这样一个问题:如图1,在四边形ABCD中,∠B=∠C=90°,E是BC的中点,AE、DE分别平分∠DAB、∠CDA.求证:AD=AB+CD.
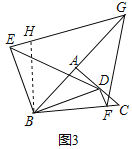
小明经探究发现,在AD上截取AF=AB,连接EF(如图2),从而可证△AEF≌△AEB,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法,解决下面的问题:
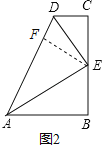
(2)如图3,△ABC是等腰直角三角形,∠A=90°,点D为边AC上任意一点(不与点A、B重合),以BD为腰作等腰直角△BDE,∠DBE=90°.过点E作BE⊥EG交BA的延长线于点G,过点D作DF⊥BD,交BC于点F,连接FG,猜想EG、DF、FG之间的数量关系,并证明.
【答案】(1)证明见解析;(2)猜想EG=DF+FG,理由见解析.
【解析】
(1)如图2,作辅助线EF,使AB=AF,构建全等三角形,△AEF≌△AEB,△DEF≌△DEC,得出FD=CD,从而得出结论;(2)猜想EG=DF+FG,在EG上截取EH=DF,连接BH,根据已知条件证明 △BEH≌△BDF,找出∠ABH=45°,再证明△BGH≌△BGF,即可得出结论.
(1)证明;在AD上截取AF=AB,连接EF,如图2所示:
∵AE、DE分别平分∠DAB、∠CDA,
∴∠BAE=∠FAE,∠CDE=∠FDE,
在△AEF和△AEB中,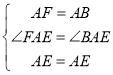 ,
,
∴△AEF≌△AEB(SAS),
∴∠AFE=∠B=90°,
∴∠DFE=90°,
在△DEF和△DEC中,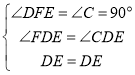 ,
,
∴△DEF≌△DEC(AAS),
∴FD=CD,
∵AD=AF+FD,
∴AD=AB+CD;
(2)解:猜想EG=DF+FG,理由如下:
在EG上截取EH=DF,连接BH,如图3所示:
∵BE⊥EG,DF⊥BD,
∴∠BEH=∠BDF=90°,
∵△BDE是等腰直角三角形,
∴BE=BD,∠EBD=90°,
在△BEH和△BDF中,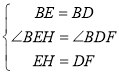 ,
,
∴△BEH≌△BDF(SAS),
∴BH=BF,∠EBH=∠DBF,
∴∠EBH+∠HBD=∠DBF+∠HBD,
∴∠EBH=∠HBC=90°,
∵△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABH=45°,
在△BGH和△BGF中,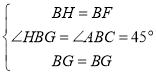 ,
,
∴△BGH≌△BGF(SAS),
∴GH=GF,
∵EG=EH+GH,
∴EG=DF+FG.

 名校课堂系列答案
名校课堂系列答案【题目】某公司有10名工作人员他们的月工资情况如表(其中x为未知数),他们的月平均工资是2.3万元,根据表中信息计算该公司工作人员的月工资的中位数和众数分别是( )
职位 | 经理 | 副经理 | A职员 | B职员 | C职员 |
人数 | 1 | 2 | 2 | 4 | 1 |
月工资(万元/人) | 5 | 3 | 2 | x | 0.8 |
A. 2,4 B. 1.9,1.8 C. 2,1.8 D. 1.8,1.9