题目内容
【题目】如图,△ABC中,∠ABC=90°,AC=25cm,BC=15cm
(1)设点P在AB上,若∠PAC =∠PCA.求AP的长;
(2)设点M在AC上.若△MBC为等腰三角形,求AM的长.

【答案】(1)![]() ;(2)10,7,
;(2)10,7,![]()
【解析】
(1)根据勾股定理求出AB,由∠PAC =∠PCA推出PA=PC,设PA=PC=x,则PB=20-X,再利用勾股定理求出x即可;
(2)过B作BN⊥AC,根据△MBC为等腰三角形分情况讨论,得出BC=CM,BC=BM,BM=CM三种情况,然后分别求AM出AM即可
解:(1)∵△ABC中,∠ABC=90°,AC=25cm,BC=15cm
∴![]()
∵∠PAC =∠PCA
∴PA=PC
设PA=PC=x,则PB=20-X
在RtPBC中
![]() 即
即![]()
解得![]() 即PA=
即PA=![]() ;
;
(2)∵△MBC为等腰三角形
∴①当BC=CM时,此时有
∴AM=AC-CM=25-15=10;
②当BC=BM时,此时
如下图过B作BN⊥AC
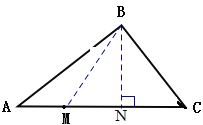
![]()
∴BN=12
∴![]() 即
即![]()
∴CN=9
∴CM=2CN=18
∴AM=25-18=7;
③当BM=CM时
∴∠MBC=∠MCB
又∠MBC+∠ABM=90°,∠MCB+∠BAC=90°
∴∠BAC=∠ABM
∴AM=BM
∴AM=CM=![]() .
.

【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.




