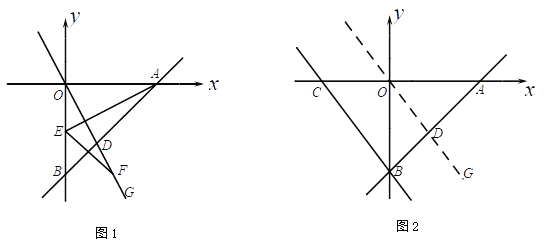��Ŀ����
����Ŀ����֪������y=ax2+bx����A��1��4����B����3��0��������A��ֱ��AC��x�ᣬ������������һ��C����x������һ��D��4��0��������CD��

��1���������ߵı���ʽ��
��2�������������ϴ��ڵ�Q��ʹ��CDƽ�֡�ACQ���������Q�����ꣻ
��3����ֱ��CD���·�����������ȡһ��N������N��NG��y�ύCD�ڵ�G����NGΪֱ����Բ��ֱ��CD�Ͻص���GH������GH�����ֵ�Ƕ��٣�
��4��һ����P��C���������ÿ��1����λ���ȵ��ٶ���C��A��D�˶������߶�CD�ϻ���һ����M�����Ƿ����ijһʱ��ʹPM+AM=4�������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��ֱ��CE�ı���ʽΪy=��![]() x��
x��![]() ����2����Q����������
����2����Q����������![]() ����
����![]() ������3����GH�����ֵ
������3����GH�����ֵ![]() ����4�����ڣ�t��ֵΪ3��7
����4�����ڣ�t��ֵΪ3��7
��������
��1���ɵ�A��B�����꣬���ô���ϵ����������������ߵı���ʽ��
��2�����ö��κ���ͼ���ϵ���������������C�����꣬��ϵ�A��D������ɵó�AC��AD�ij���ȡ��E����1��0��������CE���������ڵ�Q�����ı���ACEDΪ���Σ��ɵ�C��E�����꣬���ô���ϵ���������ֱ��CE�ı���ʽ������ֱ��CE�������߱���ʽ�ɷ����飬ͨ���ⷽ���鼴�������Q�����ꣻ
��3���ɵ�C��D�����꣬���ô���ϵ���������ֱ��CD�ı���ʽ�����N������Ϊ��x��x2+3x�������G������Ϊ��x����![]() x+2���������ɵó�NG=��x2��
x+2���������ɵó�NG=��x2��![]() x+2�����ö��κ��������ʿ����NG�����ֵ����NGΪֱ������O�䣬ȡGH���е�F������O��F����O��F��BC��ͨ����ֱ�������οɵó�GH=
x+2�����ö��κ��������ʿ����NG�����ֵ����NGΪֱ������O�䣬ȡGH���е�F������O��F����O��F��BC��ͨ����ֱ�������οɵó�GH=![]() NG������NG�����ֵ���������GH�����ֵ��
NG������NG�����ֵ���������GH�����ֵ��
��4��ȡ��E����1��0��������CE��AE������E��EP1��AC�ڵ�P1����CD�ڵ�M1������E��EP2��AD�ڵ�P2����CD�ڵ�M2����AC��x�ἰ��A������ɵó�EP1=4�������εĶԳ��Կɵó�EP2=4�����ݵ�C�͵�E������ɵó�CP1��DP2�ij��ȣ��ٽ��AC��AD�ij��������t��ֵ������ý⣮
�⣺��1����������y=ax2+bx����A��1��4����B����3��0����
��![]() ����ã�a=1,b=3,
����ã�a=1,b=3,
�������ߵı���ʽΪy=x2+3x��
��2����y=4ʱ����x2+3x=4��
��ã�x1=��4��x2=1��
���C����������4��4����
��AC=1������4��=5��
��A��1��4����D��4��0����
��AD=5��
ȡ��E����1��0��������CE���������ڵ�Q����ͼ1��ʾ��
��AC=5��DE=4������1��=5��AC��DE��
���ı���ACEDΪƽ���ı��Σ�
��AC=AD��
���ı���ACEDΪ���Σ�
��CDƽ�֡�ACQ��
��ֱ��CE�ı���ʽΪy=mx+n��m��0����
��C����4��4����E����1��0������y=mx+n���ã�
![]() ����ã�
����ã�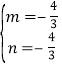 ��
��
��ֱ��CE�ı���ʽΪy=��![]() x��
x��![]() ��
��
����ֱ��CE�������߱���ʽ�ɷ����飬�ã�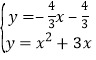 ��
��
��ã�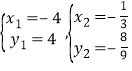 ��
��
���Q����������![]() ����
����![]() ����
����
��3����ֱ��CD�ı���ʽΪy=kx+c��k��0����
��C����4��4����D��4��0������y=kx+c���ã�
![]() ����ã�
����ã�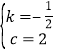 ��
��
��ֱ��CD�ı���ʽΪy=��![]() x+2��
x+2��
���N��������x��x2+3x�������G��������x����![]() x+2����
x+2����
��NG=��![]() x+2����x2+3x��=��x2��
x+2����x2+3x��=��x2��![]() x+2=����x+
x+2=����x+![]() ��2+
��2+![]() ��
��
����1��0��
�൱x=��![]() ʱ��NGȡ���ֵ�����ֵΪ
ʱ��NGȡ���ֵ�����ֵΪ![]() ��
��
��NGΪֱ������O����ȡGH���е�F������O��F����O��F��BC����ͼ2��ʾ��
��ֱ��CD�ı���ʽΪy=��![]() x+2��NG��y�ᣬO��F��BC��
x+2��NG��y�ᣬO��F��BC��
��tan��GO��F=![]() =
=![]() ��
��
��![]() ��
��
��GH=2GF=![]() O��G=
O��G=![]() NG��
NG��
����GH�����ֵΪ![]() ��
��![]() =
=![]() ��
��
��4��ȡ��E����1��0��������CE��AE������E��EP1��AC�ڵ�P1����CD�ڵ�M1������E��EP2��AD�ڵ�P2����CD�ڵ�M2����ͼ3��ʾ��
���ı���ACEDΪ���Σ�
����A��E����CD�Գƣ�
��AM=EM��
��AC��x�ᣬ��A������Ϊ��1��4����
��EP1=4��
�����εĶԳ��Կ�֪EP2=4��
�ߵ�E������Ϊ����1��0����
���P1����������1��4����
��CP1=DP2=��1������4��=3��
�֡�AC=AD=5��
��t��ֵΪ3��7��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����7�֣�ij��ѧ1000��ѧ���μ���������֪ʶ��������Ϊ���˽Ȿ�ξ����ɼ���������г�ȡ�˲���ѧ���ijɼ����÷�ȡ����������Ϊ100�֣���Ϊ��������ͳ�ƣ�����������ͼƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������Ҿֲ�����������������ʾ����������ݣ��������������⣺
�ɼ����� | Ƶ�� | Ƶ�� |
50��x��60 | 8 | 0.16 |
60��x��70 | 12 | a |
70��x��80 | �� | 0.5 |
80��x��90 | 3 | 0.06 |
90��x��100 | b | c |
�ϼ� | �� | 1 |
��1��д��a��b��c��ֵ��
��2���������1000��ѧ�����ж����˵ľ����ɼ�������70�֣�
��3����ѡȡ�������У��Ӿ����ɼ���80�����ϣ���80�֣���ͬѧ�������ȡ����ͬѧ�μӻ���֪ʶ�������������ȡ��2��ͬѧ����ͬһ��ĸ��ʣ�