Question

【题目】两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A,E,F在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同，现消防员将水流抛物线向上平移0.4m，再向左后退了m，恰好把水喷到F处进行灭火．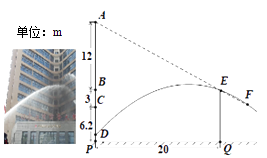

Answer 1

【答案】
【解析】根据图中的坐标系的标示，即可得出：A（0，21.2）E（20，9.2）D（0，1.2）F（ｘF，6.2）
∵A,E,F在同一直线上.
∴lAE：ｙ＝－０.６ｘ＋２１.２
代入F点坐标，即可ｘF＝２５，即F（25，6.2）
设抛物线解析式y=ax2+bx+c
代入D、E、F，即可得出y=-0.04x2+1.2x+1.2=-0.04（x-15）2+10.2
现消防员将水流抛物线向上平移0.4m，再向左后退了am
则，y=-0.04（x-15+a）2+10.2+0.4
代入F（25，6.2）
6.2=-0.04（25-15+a）2+10.2+0.4
解得x1= 10，x2=- 10（舍）
先根据题意列出AEF的直线解析式，得出E点坐标，即可得出抛物线的解析式，根据函数的平移变化：上加下减，左加右减。