题目内容
【题目】节约1度电，可以减少0.785千克碳排放．某省从2018年6月1日起执行新的居民生活用电价格，一户一表居民用户将实施阶梯式累进电价：月用电量低于50千瓦时(含50千瓦时)部分不调整，电价每千瓦时0.53元；月用电量在51～200千瓦时部分，电价每千瓦时上调0.03元；月用电量超过200千瓦时部分，电价每千瓦时上调0.10元．
小明家属一户一表居民用户，将实施阶梯式累进电价.7月份至8月份的电费缴款情况如下表：
计算日期 | 上期示度 | 本期示度 | 电量 | 金额(元) |
20180710 | 3 230 | 3 296 | 66 | 34.98 |
20180810 | 3 296 | 3 535 | 239 | 135.07 |
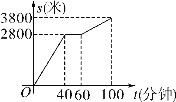
(1)根据上述资料对阶梯式累进电价的描述，设电量为x千瓦时，金额为y元，表示出金额对于电量的函数关系，并画出图象．
(2)解释小明家8月份电费的计算详情．
(3)为节约用电，小明对以后制订了详细的用电计划，如果实际每天比计划多用2千瓦时，下月用电量将会超过240千瓦时；如果实际每天比计划节约2千瓦时，那么下月用电量将会不超过180千瓦时，下月(30天)每天用电量应控制在什么范围内？
【答案】(1)见解析；(2)见解析；(3)下月每天用电量应控制在大于6千瓦时小于或等于8千瓦时范围内．
【解析】
（1）读懂题意，列式得出关系式，进而画出图象；
（2）读懂题意，进而解释小明家8月份电费的计算详情即可；
（3）设下月小明家的用电量是x千瓦时，根据题意求解即可．
(1)阶梯式累进电价的数学模型可用分段函数表示，设电量为x千瓦时，金额为y元，则有y＝
即y＝
函数图象如下图所示：
(2)基本部分：239×0.53＝126.67(元)；
调价部分：50～200千瓦时之间调价部分：(200－50)×0.03＝4.5(元)；
超过200千瓦时的调价部分：(239－200)×0.10＝3.9(元)；
合计调价部分电费：4.5＋3.9＝8.4(元)；
合计电费：126.67＋8.4＝135.07(元)．
(3)设下月每天用电量为x，根据题意列不等式组，得
解之，得6＜x≤8.
所以下月每天用电量应控制在大于6千瓦时小于或等于8千瓦时范围内．
【题目】某市在艺术节中组织中小学校文艺汇演，甲、乙两所学校共92名学生
其中甲校学生多于乙校学生，且甲校学生不足90名
，现准备统一购买服装参加演出，下表是某服装厂给出的演出服装价格表：
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装，一共应付5000元
（1）甲、乙两校各有多少名学生准备参加汇演？
（2）如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？
（3）如果甲校有10名学生被调去参加书法绘画比赛不能参加演出，请你为两校设计购买服装方案，并说明哪一种最省钱．
