题目内容
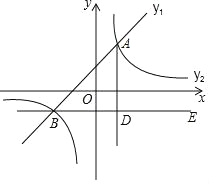
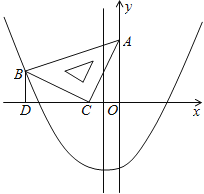
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0).如图17所示,B点在抛物线![]() 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() (3)存在,P1(
(3)存在,P1(![]() ,
,![]() )、P2(
)、P2(![]() ,
,![]() )
)
【解析】
(1)由等腰直角三角形的性质,平角定义,直角三角形两锐角的关系,可由AAS证得。
(2)求出点B的坐标,由点B、C的坐标,用待定系数法可求BC所在直线的函数关系式。
(3)分点C为直角顶点和点A为直角顶点两种情况讨论即可。
解:(1)证明:∵∠BCD+∠ACO=90°,∠ACO+∠OAC=90°,
∴∠BCD=∠OAC。
∵△ABC为等腰直角三角形 ,∴BC=AC。
在△BDC和△COA中,∠BDC=∠COA=90°,∠BCD=∠OAC,BC=AC,
∴△BDC≌△COA(AAS)。
(2)∵C点坐标为 (-1,0),∴BD=CO=1。
∵B点横坐标为-3,∴B点坐标为 (-3,1)。
设BC所在直线的函数关系式为y=kx+b,
∴![]() ,解得
,解得![]() 。∴BC所在直线的函数关系式为y=-
。∴BC所在直线的函数关系式为y=-![]() x-
x-![]() 。
。
(3)存在 。
∵y=![]() x2+
x2+![]() x-2=
x-2=![]() (x+
(x+![]() )2x-
)2x-![]() ,∴对称轴为直线x=-
,∴对称轴为直线x=-![]() 。
。
若以AC为直角边,点C为直角顶点,对称轴上有一点P1,使CP1⊥AC,
∵BC⊥AC,∴点P1为直线BC与对轴称直线x=-![]() 的交点。
的交点。
由题意可得:![]() , 解得,
, 解得,![]() 。∴P1(-
。∴P1(-![]() ,-
,-![]() )。
)。
若以AC为直角边,点A为直角顶点,对称轴上有一点P2,使AP2⊥AC,
则过点A作A P2∥BC,交对轴称直线x=-![]() 于点P2,
于点P2,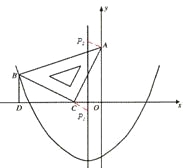
∵CD=OA,∴A(0,2)。
设直线AP2的解析式为:y=-![]() x+m,把A(0,2)代入得m=2。
x+m,把A(0,2)代入得m=2。
∴直线AP2的解析式为:y=-![]() x+2。
x+2。
由题意可得:![]() ,解得,
,解得,![]() 。∴P2(-
。∴P2(-![]() ,
,![]() )。
)。
∴P点坐标分别为P1(-![]() ,-
,-![]() )、P2(-
)、P2(-![]() ,
,![]() )。
)。

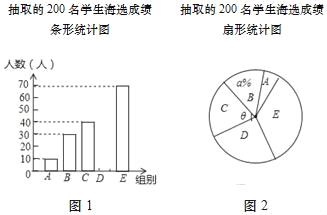
【题目】《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x≤100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
(4)经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?