题目内容
如图1,点E是矩形ABCD边BC的中点,将△ABE沿AE翻折得△AFE
(1)如图1,若折痕AE=5
,tan∠FEC=
,求线段FC的长.
(2)如图2,连接AC与BF交于点M,AE与BF交于点G,延长CG交AB于点N,连接MN,求证:∠BNG=∠AMG.
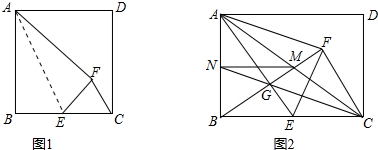
(1)如图1,若折痕AE=5
| 5 |
| 4 |
| 3 |
(2)如图2,连接AC与BF交于点M,AE与BF交于点G,延长CG交AB于点N,连接MN,求证:∠BNG=∠AMG.

考点:四边形综合题
专题:
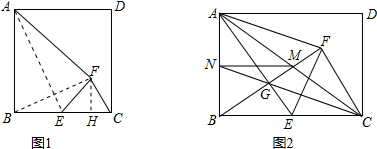
分析:(1)连接BF,过点F作FH⊥BC于H,先由正切函数的定义设FH=4k,则EH=3k,由勾股定理,得EF=5k,由折叠的性质得EC=BE=EF=5k,CH=2k,BF⊥AE,再根据勾股定理的逆定理得出∠BFC=90°,然后由两角对应相等的两三角形相似证明△FHC∽△ABE,根据相似三角形对应边成比例得到
=
,即可求出FC的长;
(2)先由两角对应相等的两三角形相似证明△BEG∽△AEB,得出
=
,由BE=CE,得到
=
,又∠CEG=∠AEC,则△CEG∽△AEC,则∠CGE=∠ACE=∠AGN,再根据等角的余角相等得出∠MAB=∠NGB,又∠ABM=∠GBN,则△ABM∽△GBN,即可得出∠BNG=∠AMG.
| FC |
| AE |
| HC |
| BE |
(2)先由两角对应相等的两三角形相似证明△BEG∽△AEB,得出
| BE |
| AE |
| GE |
| BE |
| CE |
| AE |
| GE |
| CE |
解答:解:(1)如图1,连接BF,过点F作FH⊥BC于H,则∠FHE=∠FHC=90°.
∵tan∠FEC=
,
∴设FH=4k,则EH=3k,
在Rt△HEF中,由勾股定理,得EF=5k.
∵点E是矩形ABCD边BC的中点,将△ABE沿AE翻折得△AFE,
∴EC=BE=EF=5k,CH=2k,BF⊥AE.
在Rt△HCF中,由勾股定理,得FC2=FH2+HC2=16k2+4k2=20k2,
在Rt△HBF中,由勾股定理,得FB2=FH2+BH2=16k2+64k2=80k2,
∵BC2=100k2,
∴FC2+FB2=BC2,
∴∠BFC=90°,CF⊥BF,
∵BF⊥AE,
∴CF∥AE,
∴∠FCH=∠AEB,
又∵∠FHC=∠ABE,
∴△FHC∽△ABE,
 ∴
∴
=
,即
=
,
∴FC=2
;
(2)证明:如图2,由(1)知BF⊥AE,
∴∠BGE=90°,
∴∠BGE=∠ABE=90°,
又∵∠BEG=∠AEB,
∴△BEG∽△AEB,
∴
=
,
∵BE=CE,
∴
=
,
又∵∠CEG=∠AEC,
∴△CEG∽△AEC,
∴∠CGE=∠ACE=∠AGN.
∵∠ACE+∠MAB=90°,∠AGN+∠NGB=90°,
∴∠MAB=∠NGB,
又∵∠ABM=∠GBN,
∴△ABM∽△GBN,
∴∠BMA=∠BNG,
即∠BNG=∠AMG.
∵tan∠FEC=
| 4 |
| 3 |
∴设FH=4k,则EH=3k,
在Rt△HEF中,由勾股定理,得EF=5k.
∵点E是矩形ABCD边BC的中点,将△ABE沿AE翻折得△AFE,
∴EC=BE=EF=5k,CH=2k,BF⊥AE.
在Rt△HCF中,由勾股定理,得FC2=FH2+HC2=16k2+4k2=20k2,
在Rt△HBF中,由勾股定理,得FB2=FH2+BH2=16k2+64k2=80k2,
∵BC2=100k2,
∴FC2+FB2=BC2,
∴∠BFC=90°,CF⊥BF,
∵BF⊥AE,
∴CF∥AE,
∴∠FCH=∠AEB,
又∵∠FHC=∠ABE,
∴△FHC∽△ABE,
 ∴
∴| FC |
| AE |
| HC |
| BE |
| FC | ||
5
|
| 2k |
| 5k |
∴FC=2
| 5 |
(2)证明:如图2,由(1)知BF⊥AE,
∴∠BGE=90°,
∴∠BGE=∠ABE=90°,
又∵∠BEG=∠AEB,
∴△BEG∽△AEB,
∴
| BE |
| AE |
| GE |
| BE |
∵BE=CE,
∴
| CE |
| AE |
| GE |
| CE |
又∵∠CEG=∠AEC,
∴△CEG∽△AEC,
∴∠CGE=∠ACE=∠AGN.
∵∠ACE+∠MAB=90°,∠AGN+∠NGB=90°,
∴∠MAB=∠NGB,
又∵∠ABM=∠GBN,
∴△ABM∽△GBN,
∴∠BMA=∠BNG,
即∠BNG=∠AMG.
点评:本题考查了矩形的性质,锐角三角函数的定义,折叠的性质,平行线的判定与性质,勾股定理及其逆定理,相似三角形的判定与性质,余角的性质等知识,综合性较强,难度较大.准确作出辅助线是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
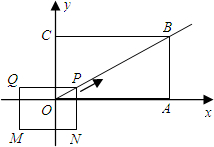 已知矩形OABC的顶点O(0,0)、A(4,0)、B(4,3).动点P从O出发,以每秒1个单位的速度,沿射线OB方向运动.设运动时间为t秒.
已知矩形OABC的顶点O(0,0)、A(4,0)、B(4,3).动点P从O出发,以每秒1个单位的速度,沿射线OB方向运动.设运动时间为t秒.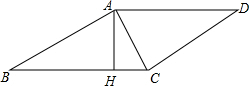 如图,在菱形ABCD中,AB=13cm,BC边上的高AH=5cm,那么对角线AC的长为
如图,在菱形ABCD中,AB=13cm,BC边上的高AH=5cm,那么对角线AC的长为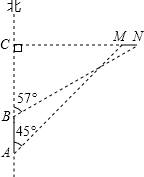 钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设N、M为该岛的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东57°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.(精确到0.1海里)参考数据:sin57°=0.84,cos57°=0.54,tan57°=1.54.
钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设N、M为该岛的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东57°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.(精确到0.1海里)参考数据:sin57°=0.84,cos57°=0.54,tan57°=1.54.