ЬтФПФкШн
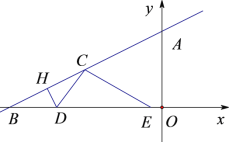
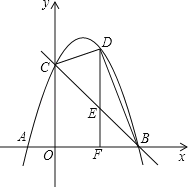
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЕуAЃЈ4ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ4ЃЉЃЌCЪЧABжаЕуЃЌСЌНгOCЃЌНЋЁїAOCШЦЕуAЫГЪБеыа§зЊЃЌЕУЕНЁїAMNЃЌМЧа§зЊНЧЮЊІСЃЌЕуOЃЌCЕФЖдгІЕуЗжБ№ЪЧMЃЌNЃЎСЌНгBMЃЌPЪЧBMжаЕуЃЌСЌНгOPЃЌPNЃЎ
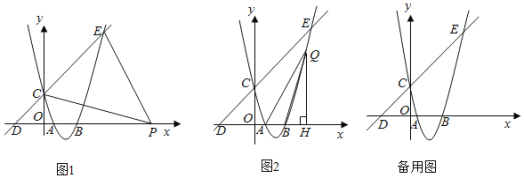
ЃЈЂёЃЉШчЭМЂйЃЎЕБІСЃН45ЁуЪБЃЌЧѓЕуMЕФзјБъЃЛ
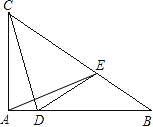
ЃЈЂђЃЉШчЭМЂкЃЌЕБІСЃН180ЁуЪБЃЌЧѓжЄЃКOPЃНPNЧвOPЁЭPNЃЛ
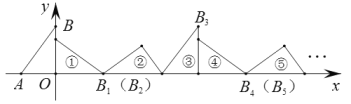
ЃЈЂѓЃЉЕБЁїAOCа§зЊжСЕуBЃЌMЃЌNЙВЯпЪБЃЌЧѓЕуMЕФзјБъЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ

ЁОД№АИЁПЃЈЂёЃЉMЃЈ4Љ2![]() ЃЌ2
ЃЌ2![]() ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ2ЃЌ2
ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ2ЃЌ2![]() ЃЉЛђЃЈ2ЃЌЉ2
ЃЉЛђЃЈ2ЃЌЉ2![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈЂёЃЉШчЭМЂйжаЃЌЙ§ЕуMзїMDЁЭOAгкDЃЎНтжБНЧШ§НЧаЮЧѓГіODЃЌOMМДПЩНтОіЮЪЬтЃЎ
ЃЈЂђЃЉШчЭМЂкЃЌЕБІСЃН180ЁуЪБЃЌЕуBЃЌAЃЌNЙВЯпЃЌOЃЌAЃЌMЙВЯпЃЌРћгУжБНЧШ§НЧаЮаББпжаЯпЖЈРэМДПЩНтОіЮЪЬтЃЎ
ЃЈЂѓЃЉЗжСНжжЧщаЮЃКЂйШчЭМЂл1жаЃЌЕБЕуMдкЯпЖЮBNЩЯЪБЃЌЂкШчЭМЂл2жаЃЌЕБЕуNдкЯпЖЮBMЩЯЪБЃЌЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЎ
ЃЈЂёЃЉШчЭМЂйжаЃЌЙ§ЕуMзїMDЁЭOAгкDЃЎ
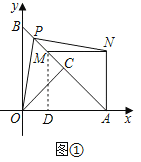
ЁпAЃЈ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌ
ЁрOAЃНOBЃН4ЃЌ
ЁпCЪЧABЕФжаЕуЃЌ
ЁрOCЃНCBЃНCAЃН![]() ABЃЌЧвOCЁЭABЃЌ
ABЃЌЧвOCЁЭABЃЌ
ЁрЁїAOCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЕБІСЃН45ЁуЪБЃЌЕуMдкABЩЯЃЌ
гЩа§зЊПЩжЊЃКЁїAOCЁеЁїAMNЃЌ
ЁрAMЃНOAЃН4ЃЎMDЃНADЃН![]() AMЃН2
AMЃН2![]() ЃЌ
ЃЌ
ЁрODЃНOAЃНADЃН4Љ2![]() ЃЌ
ЃЌ
ЁрMЃЈ4Љ2![]() ЃЌ2
ЃЌ2![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈЂђЃЉШчЭМЂкЃЌЕБІСЃН180ЁуЪБЃЌЕуBЃЌAЃЌNЙВЯпЃЌOЃЌAЃЌMЙВЯпЃЌ

ЁпЁЯBNMЃНЁЯBOMЃН90ЁуЃЌPЪЧBMЕФжаЕуЃЌ
ЁрOPЃНPNЃНPBЃНPMЃЌ
ЁрЁЯPMNЃНЁЯPNMЃЌЁЯPOBЃНЁЯPBOЃЌ
ЁпЁЯNPMЃН180ЁуЉ2ЁЯPMNЃЌЁЯBPOЃН180ЁуЉ2ЁЯPBOЃЌ
ЁрЁЯMPN+ЁЯBPOЃН360ЁуЉ2ЃЈЁЯPMN+ЁЯPBOЃЉ
ЁрЁЯMPN+ЁЯBPOЃН360ЁуЉ2ЃЈ45Ёу+ЁЯPMO+ЁЯPBOЃЉЃЌ
ЁпЁЯPMO+ЁЯPBOЃН90ЁуЃЌ
ЁрЁЯMPN+ЁЯBPOЃН90ЁуЃЌ
ЁрЁЯOPNЃН180ЁуЉЃЈЁЯMPN+ЁЯBPOЃЉЃН90ЁуЃЌ
ЁрOPЁЭPNЃЎ
ЃЈЂѓЃЉЂйШчЭМЂлЉ1жаЃЌЕБЕуMдкЯпЖЮBNЩЯЪБЃЌ
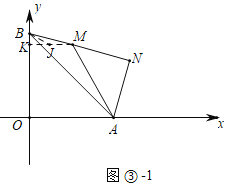
дкRtЁїABNжаЃЌЁпABЃН4![]() ЃЌANЃН2
ЃЌANЃН2![]() ЃЌ
ЃЌ
ЁрABЃН2ANЃЌ
ЁрЁЯABNЃН30ЁуЃЌ
ЁрBNЃН![]() ANЃН2
ANЃН2![]() ЃЌBMЃНBNЃНMNЃН2
ЃЌBMЃНBNЃНMNЃН2![]() Љ2
Љ2![]() ЃЌ
ЃЌ
Й§ЕуMзїMKЁЭOBгкKЃЌдкMKЩЯНиШЁвЛЕуJЃЌЪЙЕУBJЃНMJЃЌЩшBKЃНaЃЌ
ЁпЁЯABOЃН45ЁуЃЌ
ЁрЁЯMBKЃН75ЁуЃЌЁЯKMBЃН15ЁуЃЌ
ЁпJBЃНJMЃЌ
ЁрЁЯJBMЃНЁЯJMBЃН15ЁуЃЌ
ЁрЁЯBJKЃНЁЯJBM+ЁЯJMBЃН30ЁуЃЌ
ЁрBJЃНJMЃН2aЃЌKJЃН![]() aЃЌ
aЃЌ
ЁпBM2ЃНBK2+KM2ЃЌ
ЁрЃЈ2![]() Љ2
Љ2![]() ЃЉ2ЃНa2+ЃЈ2a+
ЃЉ2ЃНa2+ЃЈ2a+![]() aЃЉ2ЃЌ
aЃЉ2ЃЌ
НтЕУaЃН4Љ2![]() ЃЈИКИљвбОЩсЦњЃЉЃЌ
ЃЈИКИљвбОЩсЦњЃЉЃЌ
ЁрKMЃН2a+![]() aЃН2ЃЌOKЃН2
aЃН2ЃЌOKЃН2![]() ЃЌ
ЃЌ
ЁрMЃЈ2ЃЌ2![]() ЃЉЃЌ
ЃЉЃЌ
ЂкШчЭМЂлЉ2жаЃЌЕБЕуNдкЯпЖЮBMЩЯЪБЃЌЭЌЗЈПЩЕУMЃЈ2ЃЌЉ2![]() ЃЉЃЌ
ЃЉЃЌ
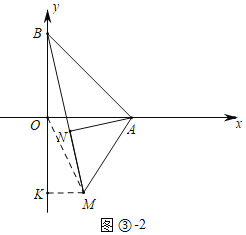
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ2ЃЌ2![]() ЃЉЛђЃЈ2ЃЌЉ2
ЃЉЛђЃЈ2ЃЌЉ2![]() ЃЉЃЎ
ЃЉЃЎ