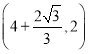ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЕФЭМЯѓЃЌОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉШ§ЕуЃЌЙ§ЕуCЃЌDЃЈЉ3ЃЌ0ЃЉЕФжБЯпгыХзЮяЯпЕФСэвЛНЛЕуЮЊEЃЎ
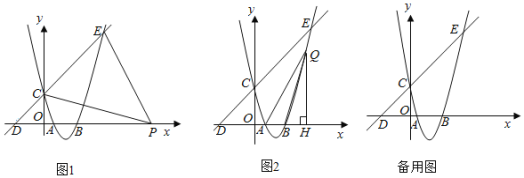
ЃЈ1ЃЉЧыФужБНгаДГіЃК
ЂйХзЮяЯпЕФНтЮіЪНЁЁ ЁЁЃЛ
ЂкжБЯпCDЕФНтЮіЪНЁЁ ЁЁЃЛ
ЂлЕуEЕФзјБъЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЛ
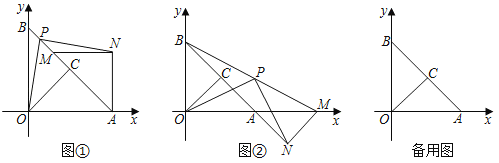
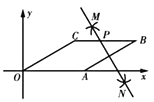
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуPЪЧxжсЩЯвЛЖЏЕуЃЌСЌНгPCЃЌPEЃЌдђЕБЕуPЮЛгкКЮДІЪБЃЌПЩЪЙЕУЁЯCPEЃН45ЁуЃЌЧыФуЧѓГіДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуQЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌзїQHЁЭxжсгкHЃЌСЌНгQAЃЌQBЃЌЕБQBЦНЗжЁЯAQHЪБЃЌЧыФужБНгаДГіДЫЪБЕуQЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйyЃНx2Љ4x+3ЃЌЂкyЃНx+3ЃЌЂлЃЈ5ЃЌ8ЃЉЃЛЃЈ2ЃЉP1ЃЈ1ЃЌ0ЃЉЃЌP2ЃЈ9ЃЌ0ЃЉЃЛЃЈ3ЃЉQЃЈ3+![]() ЃЌ3+2
ЃЌ3+2![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйМйЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНaЃЈxЉ1ЃЉЃЈxЉ3ЃЉЃЌНЋAЃЌBДњШыЃЌМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЂкЩшжБЯпCDЕФНтЮіЪНЮЊyЃНkx+bЃЌНЋCЃЌDДњШыПЩЕУжБЯпCDЕФНтЮіЪНЃЛ
ЂлСЊСЂСНИіНтЮіЪНПЩЕУEЕузјБъЃЛ
ЃЈ2ЃЉЙ§ЕуEзїEHЁЭxжсгкHЃЌгЩвбжЊПЩЭЦГіCDЃН![]() ЃЌDEЃН
ЃЌDEЃН![]() ЃЌECЃН
ЃЌECЃН![]() ЃЌЁїECPЁзЁїEPDЃЌгЩДЫПЩЕУPE2ЃЌИљОнЙДЙЩЖЈРэПЩЕУPHЃЌгЩДЫМДПЩЧѓГіЕуPЕФзјБъЃЛ
ЃЌЁїECPЁзЁїEPDЃЌгЩДЫПЩЕУPE2ЃЌИљОнЙДЙЩЖЈРэПЩЕУPHЃЌгЩДЫМДПЩЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉбгГЄQHЕНMЃЌЪЙЕУHMЃН1ЃЌСЌНгAMЃЌBMЃЌбгГЄQBНЛAMгкNЃЌЩшQЃЈtЃЌt2Љ4t+3ЃЉЃЌгЩЬтвтЕУЕуQжЛФмдкЕуBЕФгвВрЕФХзЮяЯпЩЯЃЌдђQHЃНt2Љ4t+3ЃЌBHЃНtЉ3ЃЌAHЃНtЉ1ЃЌгЩДЫПЩЭЦГіЁїQHBЁзЁїAHMЃЌОнДЫПЩЕУQNЁЭAMЃЌЕБBMЃНABЃН2ЪБЃЌQNДЙжБЦНЗжЯпЖЮAMЃЌДЫЪБQBЦНЗжЁЯAQHЃЌИљОнЙДЙЩЖЈРэПЩЕУtжЕЃЌМДПЩЭЦГіЕуQзјБъЃЎ
ЃЈ1ЃЉЂйЁпХзЮяЯпОЙ§AЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁрПЩвдМйЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНaЃЈxЉ1ЃЉЃЈxЉ3ЃЉЃЌ
АбCЃЈ0ЃЌ3ЃЉДњШыЕУЕНaЃН1ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2Љ4x+3ЃЛ
ЂкЩшжБЯпCDЕФНтЮіЪНЮЊyЃНkx+bЃЌдђга![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊyЃНx+3ЃЛ
ЂлгЩ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁрEЃЈ5ЃЌ8ЃЉЃЌ
ЙЪД№АИЮЊЃКyЃНx2Љ4x+3ЃЌyЃНx+3ЃЌЃЈ5ЃЌ8ЃЉЃЛ
ЃЈ2ЃЉШчЭМ1жаЃЌЙ§ЕуEзїEHЁЭxжсгкHЃЌ

ЁпCЃЈ0ЃЌ3ЃЉЃЌDЃЈЉ3ЃЌ0ЃЉЃЌEЃЈ5ЃЌ8ЃЉЃЌ
ЁрOCЃНODЃН3ЃЌEHЃН8ЃЌ
ЁрЁЯPDEЃН45ЁуЃЌCDЃН![]() ЃЌDEЃН
ЃЌDEЃН![]() ЃЌECЃН
ЃЌECЃН![]() ЃЌ
ЃЌ
ЕБЁЯCPEЃН45ЁуЪБЃЌЁпЁЯPDEЃНЁЯEPCЃЌЁЯCEPЃНЁЯPEDЃЌ
ЁрЁїECPЁзЁїEPDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPE2ЃНECEDЃН80ЃЌ
дкRtЁїEHPжаЃЌPHЃН![]() ЃН
ЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁрАбЕуHЯђзѓЛђЯђгвЦНвЦ4ИіЕЅЮЛЕУЕНЕуPЃЌ
ЁрP1ЃЈ1ЃЌ0ЃЉЃЌP2ЃЈ9ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉбгГЄQHЕНMЃЌЪЙЕУHMЃН1ЃЌСЌНгAMЃЌBMЃЌбгГЄQBНЛAMгкNЃЌ

ЩшQЃЈtЃЌt2Љ4t+3ЃЉЃЌгЩЬтвтЕУЕуQжЛФмдкЕуBЕФгвВрЕФХзЮяЯпЩЯЃЌдђQHЃНt2Љ4t+3ЃЌBHЃНtЉ3ЃЌAHЃНtЉ1ЃЌ
Ёр![]() ЃН
ЃН![]() ЃНtЉ3ЃН
ЃНtЉ3ЃН![]() ЃЌ
ЃЌ
ЁпЁЯQHBЃНЁЯAHMЃН90ЁуЃЌ
ЁрЁїQHBЁзЁїAHMЃЌ
ЁрЁЯBQHЃНЁЯHAMЃЌ
ЁпЁЯBQH+ЁЯQBHЃН90ЁуЃЌЁЯQBHЃНЁЯABNЃЌ
ЁрЁЯHAM+ЁЯABNЃН90ЁуЃЌ
ЁрЁЯANBЃН90ЁуЃЌ
ЁрQNЁЭAMЃЌ
ЁрЕБBMЃНABЃН2ЪБЃЌQNДЙжБЦНЗжЯпЖЮAMЃЌДЫЪБQBЦНЗжЁЯAQHЃЌ
дкRtЁїBHMжаЃЌBHЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрtЃН3+![]() ЃЌ
ЃЌ
ЁрQЃЈ3+![]() ЃЌ3+2
ЃЌ3+2![]() ЃЉЃЎ
ЃЉЃЎ

 ЛЅЖЏПЮЬУЯЕСаД№АИ
ЛЅЖЏПЮЬУЯЕСаД№АИ МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИ
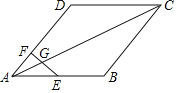
МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИЁОЬтФПЁПЫЎЙћЕъЙКНјФГжжЫЎЙћЕФГЩБОЮЊ10дЊ/ЧЇПЫЃЌОЪаГЁЕїбаЃЌЛёЕУЯњЪлЕЅМлpЃЈдЊ/ЧЇПЫЃЉгыЯњЪлЪБМфtЃЈ1ЁмtЁм15ЃЌtЮЊећЪ§ЃЉЃЈЬьЃЉжЎМфЕФВПЗжЪ§ОнШчЯТБэЃК
ЯњЪлЪБМфtЃЈ1ЁмtЁм15ЃЌtЮЊећЪ§ЃЉЃЈЬьЃЉ | 1 | 4 | 5 | 8 | 12 |
ЯњЪлЕЅМлpЃЈдЊ/ЧЇПЫЃЉ | 20.25 | 21 | 21.25 | 22 | 23 |
вбжЊpгыtжЎМфЕФБфЛЏЙцТЩЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉЪдЧѓpЙигкtЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєИУЫЎЙћЕФШеЯњСПyЃЈЧЇПЫЃЉгыЯњЪлЪБМфtЃЈЬьЃЉЕФЙиЯЕТњзувЛДЮКЏЪ§y=Ѓ2t+120ЃЈ1ЁмtЁм15ЃЌtЮЊећЪ§ЃЉЃЎ
Ђй ЧѓЯњЪлЙ§ГЬжазюДѓШеЯњЪлРћШѓЮЊЖрЩйЃП
Ђк дкЪЕМЪЯњЪлЕФЧА12ЬьжаЃЌЙЋЫООіЖЈУПЯњЪл1ЧЇПЫЫЎЙћОЭОшдљnдЊРћШѓЃЈnЃМ3ЃЉИјЁАОЋзМЗіЦЖЁБЖдЯѓЃЎЯжЗЂЯжЃКдкЧА12ЬьжаЃЌУПЬьПлГ§ОшдљКѓЕФШеЯњЪлРћШѓЫцЪБМфtЕФдіДѓЖјдіДѓЃЌЧѓnЕФШЁжЕЗЖЮЇ