��Ŀ����
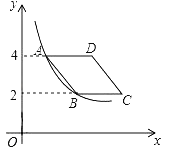
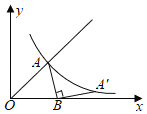
����Ŀ����ͼ����֪��������x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
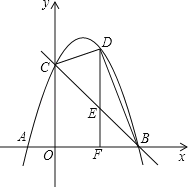
��2����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��CD�����D�ĺ�����Ϊm����BCD�����ΪS����S����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ�������S�����ֵ��
��3����֪MΪ�����߶Գ�����һ���㣬����MBC����BCΪֱ�DZߵ�ֱ�������Σ���ֱ��д����M�����꣮
���𰸡���1��y����x2+2x+3 ��2��![]() ��
��![]() ��3����1����2������1��4��
��3����1����2������1��4��
��������
��1�������߽���ʽΪy��a��x��1����x3����a��x22x3��������C������뼴����⣻
��2�������ֱ��BC�Ľ���ʽ����D��m����m2+2m+3����E��m����m+3�����õ�DE������m2+2m+3��������m+3������m2+3m��������![]() ��������⣻
��������⣻
��3����MC��б�ߡ�MB��б������������ֱ���⼴�ɣ�
�⣺��1�������߽���ʽΪy��a��x+1����x��3����a��x22x3����
����C�������,��
-3a��3����ã�a��-1��
�����߽���ʽΪy����x2+2x+3��
��2����ֱ��BC�ĺ�������ʽΪy��kx+b��
��ֱ��BC����B��3��0����C��0��3����
��![]() �����
�����![]() ��
��
��y����x+3��
��D��m����m2+2m+3����E��m����m+3����
��DE������m2+2m+3��������m+3������m2+3m��
��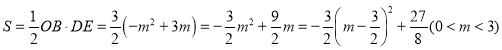 ��
��
��![]() ��
��
����![]() ʱ��S�����ֵ�����ֵ
ʱ��S�����ֵ�����ֵ![]() ��
��
��3��������y����x2+2x+3�ĶԳ���Ϊֱ��x=1
���M��1��m����
��MB2��m2+4��MC2��1+��m��3��2��BC2��18��
����MC��б��ʱ��
1+��m��3��2��m2+4+18��
��ã�m����2��
����MB��б��ʱ��
ͬ���ɵã�m��4��
�ʵ�M������Ϊ����1����2������1��4����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�