Question

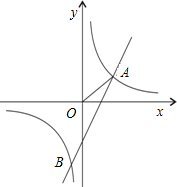如图，已知反比例函数y=

k

x

和一次函数y=2x-b图象都经过点A（1，1）
（1）求反比例函数、一次函数的表达式；
（2）如图，已知点B在第三象限，且同时在上述两个函数的图象上，求点B的坐标；
（3）在x轴上存在点P，使△AOP为等腰三角形，把符合条件的P点坐标直接写出来．

Answer 1

分析：（1）把点A（1，1）分别代入反比例函数y=

k

x

和一次函数y=2x-b，即可求出k和b的值；
（2）根据图象交点坐标满足两个解析式，把y=

1

x

和y=2x-1联立起来组成方程组，解方程组即可得到点B的坐标；
（3）分类推论：先利用勾股定理出计算出OA=

2

，当OA=OP、AO=AP、PA=PO的情况下分别计算出OP的长，即可得到符合条件的P点坐标．

解答：解：（1）把点A（1，1）分别代入反比例函数y=

k

x

和一次函数y=2x-b，
∴k=2，b=1，
∴反比例函数的解析式为：y=

1

x

；一次函数的表达式为y=2x-1；

（2）根据题意得

y= 1 x y=2x-1

，解得

x1=1 y1=1

，

x 2=- 1 2 y 2=-2

，
∴B点坐标为（-

1

2

，2）；

（3）符合条件的P点坐标有（1，0），（2，0），（-

2

，0），（

2

，0）．

点评：本题考查了点在图象上，点的横纵坐标满足图象的解析式．也考查了分类讨论思想的运用以及等腰三角形的性质．