题目内容
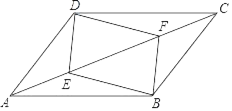
【题目】如图1,两个完全相同的三角形纸片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
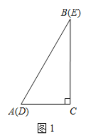
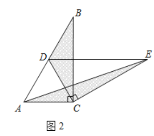

(1)操作发现:如图2,固定![]() ,使
,使![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 恰好落在
恰好落在![]() 边上时,填空:①线段
边上时,填空:①线段![]() 与
与![]() 的位置关系是________;②设
的位置关系是________;②设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是_____.
的数量关系是_____.
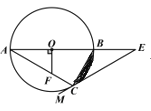
(2)猜想论证:当![]() 绕点
绕点![]() 旋转到如图3所示的位置时,请猜想(1)中
旋转到如图3所示的位置时,请猜想(1)中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
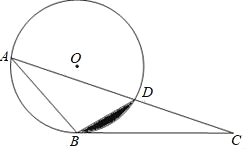
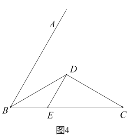
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() (如图4).若在射线
(如图4).若在射线![]() 上存在点
上存在点![]() ,使
,使![]() ,请求相应的
,请求相应的![]() 的长.
的长.
【答案】(1)DE∥AC;S1=S2;(2)成立,证明见解析;(3)BF的长为3或6.
【解析】
(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=![]() AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
(3)过点D作DF1∥BE,求出四边形BEDF1是菱形,根据菱形的对边相等可得BE=DF1,然后根据等底等高的三角形的面积相等可知点F1为所求的点,过点D作DF2⊥BD,求出∠F1DF2=60°,从而得到△DF1F2是等边三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“边角边”证明△CDF1和△CDF2全等,根据全等三角形的面积相等可得点F2也是所求的点,然后勾股定理求出EG的长,即可得解
(1)①∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°-∠B=90°-30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
故答案为:DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=AC=![]() AB,
AB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
故答案为:S1=S2;
(2)如图,过点D作DM⊥BC于M,过点A作AN⊥CE交EC的延长线于N
 ,
,
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
 ,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,
所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;
过点D作DF2⊥BD,

∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=![]() ∠ABC=30°,∠F2DB=90°,
∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,过点D作DG⊥BC于G,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB=![]() ×60°=30°,BG=
×60°=30°,BG=![]() BC=
BC=![]() ,
,
∴BD=3![]()
∴∠CDF1=180°-∠BCD=180°-30°=150°,
∠CDF2=360°-150°-60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
 ,
,
∴△CDF1≌△CDF2(SAS),
∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,
∴∠DBC=∠BDE=∠ABD=![]() ×60°=30°,
×60°=30°,
∴∠CDE=360°-∠CDF2-∠F2DB-DBE=360°-150°-90°-30°=90°,
∴∠CDG=90°-∠DCG=60°,
又∵BD=CD=3![]() ,
,
∴DG=![]() ,
,
设EG为x,则DE=2x,
![]() ,
,
解得x=1.5,
∴BE=BG-EG=4.5-1.5 =3,
∴BF1=3,BF2=BF1+F1F2=3+3=6,
故BF的长为3或6.