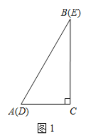Question

【题目】如图，在四边形ABCD中，，，，，点P从点B出发，沿线段BA，向点A以的速度匀速运动；点Q从点D出发，沿线段DC向点C以的速度匀速运动，已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为．

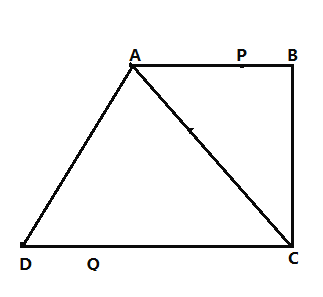
（1）连结P、Q两点，则线段PQ长的取值范围是________；

（2）当cm时，求t的值；

（3）若在线段CD上有一点E，cm，连结AC和PE．请问是否存在某一时刻使得AC平分PE？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）t的值为2或；（3）存在某一时刻使得AC平分PE，此时t的值为4．

【解析】

（1）先确认线段PQ取最大值与最小值时点P、Q的位置，再根据矩形的性质、勾股定理求解即可；

（2）先根据勾股定理求出FQ的长，再根据分两种情况：点Q在点F左侧和点Q在点F右侧，然后根据图中的建立方程求解即可得；

（3）当AC平分PE时，先根据平行线的性质得出，再根据三角形全等的判定定理与性质得出，然后分点Q在点E左侧和点Q在点E右侧，分别建立方程求解即可得．

（1）四边形ABCD中，

四边形ABCD是直角梯形

由题意可知，在点P、Q运动过程中，当点P在点B处，点Q在点D处时，线段PQ取得最大值BD；当时，线段PQ取得最小值，此时

如图1，过点A作，连接BD，则四边形ABCM是矩形

则线段PQ长的取值范围是

故答案为：；

（2）点P运动到点A所需时间为；点Q运动到C所需时间为

由题意得，

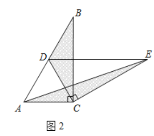
如图2，过点P作，则四边形BCFP是矩形

因，则分以下两种情况：

①当点Q在点F左侧时，

即，解得，符合题意

②当点Q在点F右侧时，即点Q在点处

则，解得，符合题意

综上，t的值为2或；

（3）存在某一时刻使得AC平分PE，求解过程如下：

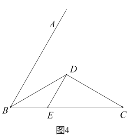
如图3，设AC与PE相交于点O

当AC平分PE时，

在和中，

由题意，分以下两种情况：

①当点Q在点E左侧时，

即，解得，符合题意

②当点Q在点E右侧时，即点Q在点处，

则，解得，不符题意，舍去

综上，存在某一时刻使得AC平分PE，此时t的值为4．