题目内容
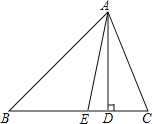
【题目】如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为6,将一块边长足够长的三角板的直角顶点放在O点处,将三角板绕着点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为( )
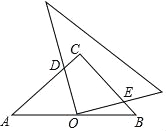
A. 7 B. 6 C. 5 D. 4
【答案】B
【解析】
连接OC,证明△OCD≌△OBE,根据全等三角形的性质得到CD=BE即可解决问题.
连接OC,
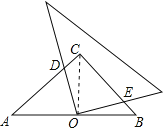
∵AC=BC,AO=BO,∠ACB=90°,
∴∠ACO=∠BCO=![]() ∠ACB=45°,OC⊥AB,∠A=∠B=45°,
∠ACB=45°,OC⊥AB,∠A=∠B=45°,
∴OC=OB,
∵∠BOE+∠EOD+∠AOD=180°,∠EOD=90°,
∴∠BOE+∠AOD=90°,
又∵∠COD+∠AOD=90°,
∴∠BOE=∠COD,
在△OCD和△OBE中,
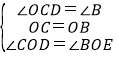 ,
,
∴△OCD≌△OBE(ASA),
∴CD=BE,
∴CD+CE=BE+CE=BC═AC=6.
故选:B.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目