题目内容
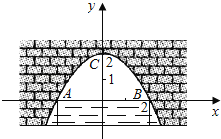
【题目】在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.
(1)求油的最大深度;
(2)如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?

【答案】(1)100mm;(2)此时油面上升了100毫米或700毫米
【解析】
(1)作OF⊥AB交AB于F,交圆于G,连接OA,由垂径定理可求AF=300 mm,再由勾股定理求出OF的长,即可求出水深GF的长;
(2)连接OC,分水面在圆心下方和圆心上方两种情况求解即可.
解:(1)作OF⊥AB交AB于F,交圆于G,连接OA,
∴AF=![]() AB=300 mm,由勾股定理得,OF=
AB=300 mm,由勾股定理得,OF=![]() =400 mm,
=400 mm,
则GF=OG﹣OF=100mm;
(2)连接OC,
∵OE⊥CD,
∴CE=400 mm,OE=![]() =300 mm,
=300 mm,
则EF=OG﹣OE﹣FG=100 mm,
同理,当CD在圆心O上方时,可得EF=700 mm.
答:此时油面上升了100毫米或700毫米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目