题目内容
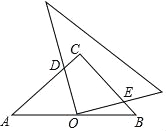
【题目】如图，已知直线
与
相离，
于点
，
，
与相交于点
，
与相切于点
，
的延长线交直线于点
．若上存在点
，使
是以
为底边的等腰三角形，则半径
的取值范围是：________．
【答案】
【解析】
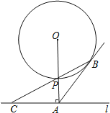
首先证明AB＝AC，再根据已知得出Q在AC的垂直平分线上，作出线段AC的垂直平分线MN，作OE⊥MN，求出OE＜r，求出r范围即可.
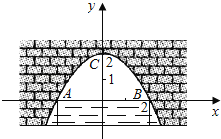
连结OB，如图1，∵AB切⊙O于点B，OA⊥AC，∴∠OBA＝∠OAC＝90°，∴∠OBP＋∠ABP＝90°，∠ACP＋∠APC＝90°，∵OP＝OB，∴∠OBP＝∠OPB，∵∠OPB＝∠APC，∴∠ACP＝∠ABC，∴AB＝AC，作出线段AC的垂直平分线MN，作OE⊥MN，如图2所示，∵
，又∵圆O与直线MN有交点，∴
，即
，∴r≥
.∵OA＝10，直线l与⊙O相离，∴r＜10，∴≤r＜10.故答案为≤r＜10.
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）
与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
【题目】如图，已知
、
分别为
的直径和弦，
为
的中点，
垂直于的延长线于
，连接
，若
，
，下列结论一定错误的是( )
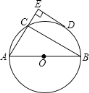
A. DE是⊙O的切线 B. 直径AB长为20cm
C. 弦AC长为16cm D. C为
的中点
【题目】某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件？
(2)通过手绘设计后全部售出，求该校这次义卖活动所获利润．
