题目内容
已知在△ABC中,∠ACB=90°,CA=CB=6
,CD⊥AB于D,点E在直线CD上,DE=
CD,点F在线段AB上,M是DB的中点,直线AE与直线CF交于N点.
(1)如图1,若点E在线段CD上,请分别写出线段AE和CM之间的位置关系和数量关系: , ;
(2)在(1)的条件下,当点F在线段AD上,且AF=2FD时,求证:∠CNE=45°;
(3)当点E在线段CD的延长线上时,在线段AB上是否存在点F,使得∠CNE=45°?若存在,请直接写出AF的长度;若不存在,请说明理由.

| 2 |
| 1 |
| 2 |
(1)如图1,若点E在线段CD上,请分别写出线段AE和CM之间的位置关系和数量关系:
(2)在(1)的条件下,当点F在线段AD上,且AF=2FD时,求证:∠CNE=45°;
(3)当点E在线段CD的延长线上时,在线段AB上是否存在点F,使得∠CNE=45°?若存在,请直接写出AF的长度;若不存在,请说明理由.

考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)延长AE交CM于点H,由等腰直角三角形的性质就可以得出△AEC≌△CMB,就可以得出∠CAE=∠BCM而得出结论;
(2)如图1,过点A作AG⊥AB,且AG=BM,连接CG、FG,延长AE交CM于H.先由等腰三角形的性质和勾股定理就可以得出FG=FM,就可以得出△CAG≌△CBM,就有CG=CM,∠ACG=∠BCM.得出∠MCG=90°.进而证明△FCG≌△FCM就可以得出结论;
(3)如图2,作BH⊥CN于H,由条件就可以得出∠ANB=∠NCB,可以得出△ADE∽△CHB,就可以求出BH的值,再得出△CDF∽△BHF就可以求出DF的值,进而求出AF的值.
(2)如图1,过点A作AG⊥AB,且AG=BM,连接CG、FG,延长AE交CM于H.先由等腰三角形的性质和勾股定理就可以得出FG=FM,就可以得出△CAG≌△CBM,就有CG=CM,∠ACG=∠BCM.得出∠MCG=90°.进而证明△FCG≌△FCM就可以得出结论;
(3)如图2,作BH⊥CN于H,由条件就可以得出∠ANB=∠NCB,可以得出△ADE∽△CHB,就可以求出BH的值,再得出△CDF∽△BHF就可以求出DF的值,进而求出AF的值.
解答:解:(1)AE⊥CM,AE=CM
理由:延长AE交CM于点H,
∵∠ACB=90°,CA=CB=6
,CD⊥AB于D,
∴∠CAB=∠CBA=∠ACD=∠BCD=45°,AD=BD=CD=
AB.
∵M是DB的中点,
∴BM=
BD.
∵DE=
CD,
∴DE=BM.
在△AEC和△CMB中
∵
,
∴△AEC≌△CMB(SAS),
∴AE=CM,∠CAE=∠BCM.
∵∠ACM+∠BCM=90°,
∴∠ACM+∠CAE=90°,
∴∠ACH=90°.
∴AH⊥CM.
∴AE⊥CM,AE=CM;
(2)如图1,过点A作AG⊥AB,且AG=BM,连接CG、FG,延长AE交CM于H.
∵∠ACB=90°,CA=CB=6
,
∴∠CAB=∠CBA=45°,AB=
=12.
∴∠GAC=∠MBC=45°.
∵CD⊥AB,
∴CD=AD=BD=
AB=6.
∵M是DB的中点,
∴DM=BM=3.
∴AG=3.
∵AF=2FD,
∴AF=4,DF=2,
∴FM=DF+DM=2+3=5.
∵AG⊥AF,
∴FG=
=
=5,
∴FG=FM.
在△CAG和△CBM中,
,
∴△CAG≌△CBM.
∴CG=CM,∠ACG=∠BCM.
∴∠MCG=∠ACM+∠ACG=∠ACM+BCM=90°.
在△FCG和△FCM中,
,
∴△FCG≌△FCM(SSS).
∴∠FCG=∠FCM.
∴∠FCM=45°.
∵AE⊥CM,
∴∠CHN=90°
∴∠CNE=45°;
(3)存在.
理由:如图2,作BH⊥CN于H,
∴∠CHB=90°.
∵CD⊥AB,
∴∠ADE=90°,
∴∠CHB=∠ADE.
∵∠ACB=90°,CA=CB=6
,
∴∠CAB=∠CBA=45°.AB=
=12.
∴∠GAC=∠MBC=45°.
∵CD⊥AB,
∴CD=AD=BD=
AB=6.
∵DE=
CD,
∴DE=3.
在Rt△ADE中,由勾股定理得 AE=3
AE=3
.
∵∠CNE=45°,
∴∠CBA=∠CNE.
∵∠AFN=∠CFB,
∴∠NAF=∠BCF.
∴△ADE∽△CHB,
∴
=
,
∴
=
,
∴BH=
.
设DF=x,则BF=6-x.
在Rt△CDF中,由勾股定理,得
CF=
.
∵∠CDF=∠BHF=90°,∠DFC=∠HFB,
∴△CDF∽△BHF,
∴
=
,
∴
=
,
∴x1=2,x2=18>6(舍去),
∴x=2.
∴AF=6+2=8.
答:AF=8.
理由:延长AE交CM于点H,
∵∠ACB=90°,CA=CB=6
| 2 |
∴∠CAB=∠CBA=∠ACD=∠BCD=45°,AD=BD=CD=
| 1 |
| 2 |
∵M是DB的中点,
∴BM=
| 1 |
| 2 |
∵DE=
| 1 |
| 2 |
∴DE=BM.
在△AEC和△CMB中
∵
|
∴△AEC≌△CMB(SAS),
∴AE=CM,∠CAE=∠BCM.
∵∠ACM+∠BCM=90°,
∴∠ACM+∠CAE=90°,
∴∠ACH=90°.
∴AH⊥CM.
∴AE⊥CM,AE=CM;
(2)如图1,过点A作AG⊥AB,且AG=BM,连接CG、FG,延长AE交CM于H.
∵∠ACB=90°,CA=CB=6
| 2 |
∴∠CAB=∠CBA=45°,AB=
| CA2+CB2 |
∴∠GAC=∠MBC=45°.
∵CD⊥AB,
∴CD=AD=BD=
| 1 |
| 2 |
∵M是DB的中点,
∴DM=BM=3.
∴AG=3.
∵AF=2FD,

∴AF=4,DF=2,
∴FM=DF+DM=2+3=5.
∵AG⊥AF,
∴FG=
| AG2+AF2 |
| 32+42 |
∴FG=FM.
在△CAG和△CBM中,
|
∴△CAG≌△CBM.
∴CG=CM,∠ACG=∠BCM.
∴∠MCG=∠ACM+∠ACG=∠ACM+BCM=90°.
在△FCG和△FCM中,
|
∴△FCG≌△FCM(SSS).
∴∠FCG=∠FCM.
∴∠FCM=45°.
∵AE⊥CM,
∴∠CHN=90°
∴∠CNE=45°;
(3)存在.
理由:如图2,作BH⊥CN于H,
∴∠CHB=90°.
∵CD⊥AB,
∴∠ADE=90°,
∴∠CHB=∠ADE.
∵∠ACB=90°,CA=CB=6
| 2 |
∴∠CAB=∠CBA=45°.AB=
| CA2+CB2 |
∴∠GAC=∠MBC=45°.
∵CD⊥AB,
∴CD=AD=BD=
| 1 |
| 2 |
∵DE=
| 1 |
| 2 |
∴DE=3.
在Rt△ADE中,由勾股定理得
 AE=3
AE=3| 5 |
∵∠CNE=45°,
∴∠CBA=∠CNE.
∵∠AFN=∠CFB,
∴∠NAF=∠BCF.
∴△ADE∽△CHB,
∴
| DE |
| BH |
| AE |
| BC |
∴
| 3 |
| BH |
3
| ||
6
|
∴BH=
| 6 |
| 5 |
| 10 |
设DF=x,则BF=6-x.
在Rt△CDF中,由勾股定理,得
CF=
| 36+x2 |
∵∠CDF=∠BHF=90°,∠DFC=∠HFB,
∴△CDF∽△BHF,
∴
| CD |
| BH |
| CF |
| BF |
∴
| 6 | ||||
|
| ||
| 6-x |
∴x1=2,x2=18>6(舍去),
∴x=2.
∴AF=6+2=8.
答:AF=8.
点评:本题考查了等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,相似三角形的判定及性质的运用,解答时证明三角形全等和相似是关键.

练习册系列答案
相关题目
 如图,已知的半径为R,C、D是直径AB同侧圆周上的两点,∠AOC=96°,∠BOD=36°,动点P在AB上,PC+PD的最小值是( )
如图,已知的半径为R,C、D是直径AB同侧圆周上的两点,∠AOC=96°,∠BOD=36°,动点P在AB上,PC+PD的最小值是( )| A、2R | ||||
B、
| ||||
C、
| ||||
D、
|
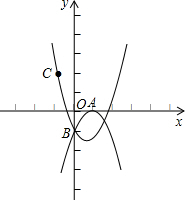 已知抛物线y=a(x-1)2+k经过A(1,0),B(0,-1),C(-1,2),D(2,1),E(4,2)这五个点中至少三个点,则这样的抛物线有( )条.
已知抛物线y=a(x-1)2+k经过A(1,0),B(0,-1),C(-1,2),D(2,1),E(4,2)这五个点中至少三个点,则这样的抛物线有( )条. 如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积.
如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积. 如图,AB、DE是⊙O的直径,点C在⊙O上,且
如图,AB、DE是⊙O的直径,点C在⊙O上,且