题目内容
【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
【答案】
(1)解:由“同族二次函数的定义”可知: ![]() 和
和 ![]() 是一对“同族二次函数”(答案不唯一);
是一对“同族二次函数”(答案不唯一);
(2)解:∵ ![]() 的图象过点A(1,1),
的图象过点A(1,1),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴ ![]() ,
,
∴ ![]() 的顶点坐标为(1,1),且
的顶点坐标为(1,1),且 ![]() ,
,
∵ ![]() 与
与 ![]() 是“同族二次函数”,
是“同族二次函数”,
∴ ![]() 的顶点坐标也为(1,1),
的顶点坐标也为(1,1),
∴ 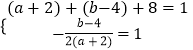 ,解得:
,解得: ![]() ,
,
∴ ![]() ,
,
又∵ ![]() 在对称轴
在对称轴 ![]() 的右侧,
的右侧,
∴当 ![]() 时,
时, ![]() 2最小=5.
2最小=5.
【解析】(1)在写函数式时,抓住若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”,即可写出函数解析式。
(2)先将点A的坐标代入y1求出y1的函数解析式,再求出y1的顶点坐标,求出y1+y2与x的函数解析式,再将(1,1)代入y1+y2与x的函数解析式,建立方程,再根据对称轴x=1建立方程,求出a、b的值,即可写出 y 2 与x的函数解析式,再根据2 ≤ x ≤ 3及二次函数的增减性求出y2的最小值.。
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯 | 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤280 | b |
三档 | x>280 | 0.82 |
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?