题目内容
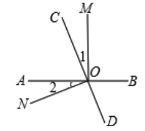
【题目】如图，直线AB、CD相交于O点，OM⊥AB；
(1)若∠1=∠2，求∠NOD；
(2)若∠1=
∠BOC，求∠AOC与∠MOD．
【答案】（1）∠NOD=90°；（2）∠AOC=60°；∠MOD=150°
【解析】
（1）根据垂直的定义可得∠AOM=90°，从而得出∠1＋∠AOC=90°，然后利用等量代换可得∠2＋∠AOC=90°，从而求出结论；
（2）根据垂直的定义可得∠AOM=∠BOM=90°，然后结合已知条件即可求出∠1，然后从而求出结论．
解：（1）∵OM⊥AB
∴∠AOM=90°
∴∠1＋∠AOC=90°
∵∠1=∠2
∴∠2＋∠AOC=90°
∴∠CON=90°
∴∠NOD=180°－∠CON=90°
（2）∵OM⊥AB
∴∠AOM=∠BOM=90°
∵∠1=
∠BOC
∴∠1=
∠BOM=30°
∴∠AOC=∠AOM－∠1=60°
∴∠MOD=180°－∠1=150°
练习册系列答案
相关题目
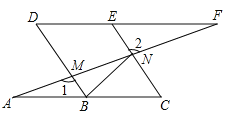
【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．
（1）求证：四边形BCED是平行四边形；
（2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．
