题目内容
【题目】如图1,△ABC中,AD⊥BC于D,CE⊥AB于E.
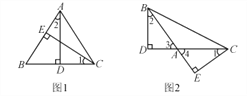
(1)猜测∠1与∠2的关系,并说明理由;
如果∠BAC是钝角,如图2,(1)中的结论是否还成立?
【答案】(1)∠1=∠2 (2)结论仍然成立
【解析】试题分析:(1)根据垂直的定义可得△ABD和△BCE是直角三角形,再根据直角三角形两锐角互余可得∠1+∠B=90°,∠2+∠B=90°,从而得解;(2)根据垂直的定义可得∠D=∠E=90°,根据直角三角形的两锐角互余可得∠1+∠4=90°,∠2+∠3=90°,再根据∠3=∠4即可得∠1=∠2.
试题解析:
(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE都是直角三角形,
∴∠1+∠B=90°,∠2+∠B=90°.
∴∠1=∠2.
(2)结论仍然成立.理由如下:
∵BD⊥AC,CE⊥AB,
∴∠D=∠E=90°.
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠3=∠4,
∴∠1=∠2.

练习册系列答案
相关题目
【题目】学校为了丰富学生课余活动开展了一次“爱我学校,唱我学校”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60B.9.60,9.60C.9.60,9.70D.9.65,9.60