题目内容
【题目】如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,在△ACD中,线段AE是CD边上的中线,连接BD.求证:CD=2BD.
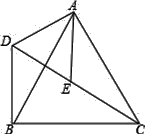
【答案】证明见解析.
【解析】试题分析:根据已知条件用“SAS”定理证明△ACE≌△ABD,可得BD=CE,由AE是CD边上的中线,可得CD=2CE,从而可证CD=2BD.
试题解析:(1)∵△ACB和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠CAE=∠BAD,
在△ACE和△ABD中,
AB=AC,∠CAE=∠BAD,AD=AE,
∴△ACE≌△ABD(SAS),
∴BD=CE,
又∵AE是CD边上的中线,
∴CD=2CE,
∴CD=2BD.

练习册系列答案
相关题目