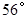题目内容
绕侧面一周,再回到
 点的最短的路线长是
点的最短的路线长是 

试题考查知识点:两点间线段最短
思路分析:把圆锥剪开平铺,利用公理“两点间线段最短”判断最短距离,然后利用三角形有关知识进行计算
具体解答过程:
如图所示。以母线OA剪开,并展开成一个扇形OABA′,连接AA′。根据公理“两点间线段最短”,AA′的线段长就是所求的最短距离。
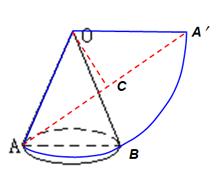
∵原圆锥的母线长OA=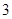 ,底面周长为L=2πr=2π×1=2π
,底面周长为L=2πr=2π×1=2π
∴扇形OABA′的半径为R=3,而弧ABA′的长度L′=L=2π,
以R=3为半径的圆的周长为2πR=2π×3=6π
∴扇形OABA′中弧ABA′所对的圆心角为∠AOA′=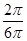 ×360°=120°
×360°=120°
做OC⊥AA′,垂足为C,
∵OA=OA′
∴∠AOC= ∠AOA′=60°,AC=A′C=
∠AOA′=60°,AC=A′C= AA′
AA′
∴AC=OA·sin∠AOC=3×sin60°=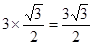
∴AA′=2AC=2×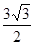 =
=
即从 点出发绕侧面一周,再回到
点出发绕侧面一周,再回到 点的最短的路线长是
点的最短的路线长是
试题点评:化繁为简,化立体为平面,这是这道题目的特点,也是一种解决问题的好思路。
思路分析:把圆锥剪开平铺,利用公理“两点间线段最短”判断最短距离,然后利用三角形有关知识进行计算
具体解答过程:
如图所示。以母线OA剪开,并展开成一个扇形OABA′,连接AA′。根据公理“两点间线段最短”,AA′的线段长就是所求的最短距离。

∵原圆锥的母线长OA=
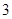 ,底面周长为L=2πr=2π×1=2π
,底面周长为L=2πr=2π×1=2π∴扇形OABA′的半径为R=3,而弧ABA′的长度L′=L=2π,
以R=3为半径的圆的周长为2πR=2π×3=6π
∴扇形OABA′中弧ABA′所对的圆心角为∠AOA′=
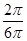 ×360°=120°
×360°=120°做OC⊥AA′,垂足为C,
∵OA=OA′
∴∠AOC=
 ∠AOA′=60°,AC=A′C=
∠AOA′=60°,AC=A′C= AA′
AA′∴AC=OA·sin∠AOC=3×sin60°=
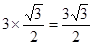
∴AA′=2AC=2×
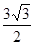 =
=
即从
 点出发绕侧面一周,再回到
点出发绕侧面一周,再回到 点的最短的路线长是
点的最短的路线长是
试题点评:化繁为简,化立体为平面,这是这道题目的特点,也是一种解决问题的好思路。

练习册系列答案
相关题目
 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为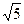 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.
 ).
).
 的度数( )
的度数( )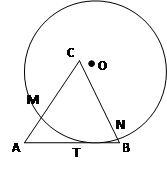
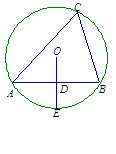
 内接于
内接于 ,若
,若 ,则
,则 的大小为 ( )
的大小为 ( )