题目内容
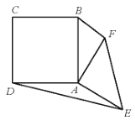
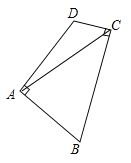
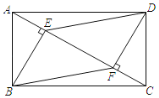
【题目】如图，在矩形
中，
，
，垂足分别为
、
，连接
、
．
（1）求证：
；
（2）判断四边形
的形状，并说明理由．
【答案】（1）见解析；（2）四边形
是平行四边形．理由见解析．
【解析】
（1）根据矩形的性质得出AB∥CD，AB＝CD，从而可得∠BAE＝∠DCF，然后利用AAS证出△ABE≌△CDF，从而得出BE＝DF；
（2）求出BE∥DF，结合BE＝DF即可证得四边形BEDF是平行四边形．
（1）证明：∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD，
∴∠BAE＝∠DCF，
∵BE⊥AC，DF⊥AC，
∴∠BEA＝∠DFC＝90°，
∴△ABE≌△CDF（AAS），
∴BE＝DF；
（2）四边形BEDF是平行四边形．
理由：∵BE⊥AC，DF⊥AC，
∴BE∥DF，
又∵BE＝DF，
∴四边形BEDF是平行四边形．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
【题目】课外阅读是提高学生素养的重要途径．某中学为了了解全校学生课外阅读情况，随机抽查了200名学生，统计他们平均每天课外阅读时间（小时）．根据每天课外阅读时间的长短分为A，B，C．D四类，下面是根据所抽查的人数绘制的两幅不完整的统计图表，请根据图中提供的信息，解答下面的问题：
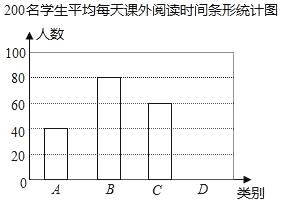
200名学生平均每天课外阅读时间统计表
类别 | 时间t（小时） | 人数 |
A | t＜0.5 | 40 |
B | 0.5≤t＜1 | 80 |
C | 1≤t＜1.5 | 60 |
D | t≥1.5 | a |
（1）求表格中a的值，并在图中补全条形统计图：
（2）该校现有1800名学生，请你估计该校共有多少名学生课外阅读时间不少于1小时？
（3）请你根据上述信息对该校提出相应的建议
