题目内容
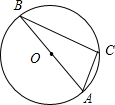 如图,⊙O是△ABC外接圆,直径AB=12,∠A=2∠B.
如图,⊙O是△ABC外接圆,直径AB=12,∠A=2∠B.(1)∠A=
(2)求BC的长(结果用根号表示);
(3)连接OC并延长到点P,使CP=OC,连接PA,画出图形,求证:PA是⊙O的切线.
分析:(1)不难看出∠C应该是直角,∠A=2∠B,那么这两个角的度数就容易求得了;
(2)直角三角形ABC中,有斜边AB的长,有三角的度数,BC的值就能求出了;
(3)此题实际上是证明PA⊥AB,由图我们不难得出△AOC是等边三角形,那么就容易证得△ABC≌△OPA,这样就能求出PA⊥AB了.
(2)直角三角形ABC中,有斜边AB的长,有三角的度数,BC的值就能求出了;
(3)此题实际上是证明PA⊥AB,由图我们不难得出△AOC是等边三角形,那么就容易证得△ABC≌△OPA,这样就能求出PA⊥AB了.
解答: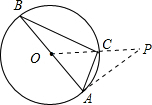 解:(1)∵∠C=90°,∠A=2∠B,
解:(1)∵∠C=90°,∠A=2∠B,
∴∠A=60°,∠B=30°;
(2)∵AB为直径,
∴∠ACB=90°,
又∵∠B=30°,
∴AC=
AB=65.
∴BC=
=6
;
(3)如图,∵OP=2OC=AB,
∵∠BAC=60°,OA=OC,
∴△OAC为等边三角形.
∴∠AOC=60°.
在△ABC和△OPA中,
∵AB=OP,∠BAC=∠POA=60°,AC=OA,
∴△ABC≌△OPA.
∴∠OAP=∠ACB=90°.
∴PA是⊙O的切线.
 解:(1)∵∠C=90°,∠A=2∠B,
解:(1)∵∠C=90°,∠A=2∠B,∴∠A=60°,∠B=30°;
(2)∵AB为直径,
∴∠ACB=90°,
又∵∠B=30°,
∴AC=
| 1 |
| 2 |
∴BC=
| AB2-AC2 |
| 3 |
(3)如图,∵OP=2OC=AB,
∵∠BAC=60°,OA=OC,
∴△OAC为等边三角形.
∴∠AOC=60°.
在△ABC和△OPA中,
∵AB=OP,∠BAC=∠POA=60°,AC=OA,
∴△ABC≌△OPA.
∴∠OAP=∠ACB=90°.
∴PA是⊙O的切线.
点评:本题主要考查了解直角三角形的应用和切线的判定等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
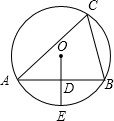 如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD=
如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD= 24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由.
24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由. (2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( )
(2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( ) (2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
(2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.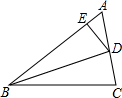 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.