题目内容
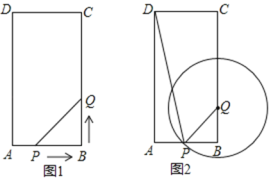
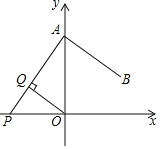
【题目】如图，在平面直角坐标系xOy中，点A（0，6），点B（4，3），P是x轴上的一个动点．作OQ⊥AP，垂足为Q，则点Q到直线AB的距离的最大值为_____．
【答案】
【解析】
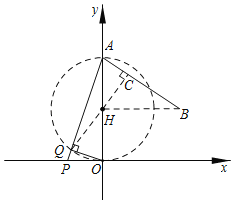
作BH⊥OA于H，则可得H（0，3），先判断点Q在以OA为直径的圆上，即可得到QH长为定值，当Q，H，C在同一直线上，且QH⊥BC时，Q点到AB的距离最大，利用面积法计算出HC＝
，则点Q到直线AB的距离的最大值为CQ＝CH+QH．
解：∵点A（0，6），点B（4，3），
∴AB＝
＝5，
如图，作BH⊥OA于H，过H作HC⊥AB于C，则H（0，3），HC＝
＝，
∴H点为OA的中点，
∵OQ⊥PA，
∴∠OQA＝90°，
∴点Q在以OA为直径的圆上，
连接QH，则QH＝
AO＝3，
如图，当Q，H，C在同一直线上，且QH⊥BC时，Q点到AB的距离最大，
此时，CQ＝QH+CH＝3+＝，
即点Q到直线AB的距离的最大值为，
故答案为：.
练习册系列答案
口算题天天练系列答案
相关题目
