题目内容
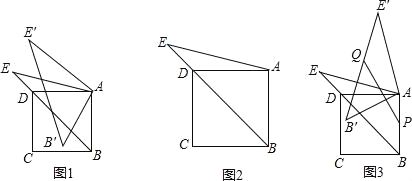
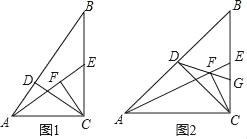
【题目】已知:如图1,△ABC中,∠ACB=90°,CD⊥AB于D,E为BC中点,CF⊥AE于F.
(1)求证:4CE2=BDAB;
(2)若2∠DCF=∠ECF,求cos∠ECF的值;
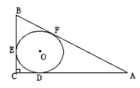
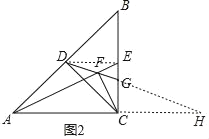
(3)如图2,DF延长线交BC于G,若AC=BC,EG=1,则DG= .
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用两组对应角分别相等的两个三角形相似可得△BCA∽△BDC,由相似三角形对应线段成比例的性质可得结论;
(2)过B作BG⊥BC交AE的延长线于G,在AE上取H,使HA=HB,利用ASA可证△ACE≌GBE,由全等三角形的性质及等腰三角形的性质可得BH=BG=HA,设AH=BH=BG=a,HE=b,作MB⊥HG,可用含![]() 的代数式表示出EG、HM和MG,由射影定理可得
的代数式表示出EG、HM和MG,由射影定理可得![]() 的关系式,根据cos∠ECF=cos∠G=
的关系式,根据cos∠ECF=cos∠G=![]() 计算即可;
计算即可;
(3)连接DE,延长DG、AC相交于H,由等腰三角形“三线合一”的性质及三角形中位线的性质可得DE=![]() AC,等量代换可得GC长,易知EC长,由等腰直角三角形的性质可得DE长,由勾股定理即可求出DG长.
AC,等量代换可得GC长,易知EC长,由等腰直角三角形的性质可得DE长,由勾股定理即可求出DG长.
解:(1)∵CD⊥AB于D,
∴∠BDC=∠ACB=90°.
∵∠DBC=∠ACB,
∴△BCA∽△BDC,
∴![]() ,
,
即BC2=BDAB.
∵E为BC中点,
∴BC=2CE,
∴4CE2=BDAB;
(2)如图1,过B作BG⊥BC交AE的延长线于G,在AE上取H,使HA=HB.
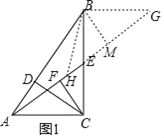
∵∠BEG=∠AEC,∠EBG=∠ACE=90°,BE=EC,
∴△ACE≌GBE(ASA),
∴∠G=∠EAC,BG=AC,
∵CD⊥AB于D,CF⊥AE于F,
∴∠DCF=∠DAF,∠ECF=∠FAC=∠G,
∴∠BFG=2∠DAC=∠FAC=∠G,
∴BH=BG=HA.
设AH=BH=BG=a,HE=b,
作MB⊥HG,则MH=MG,EG=a+b,HM=MG=b+![]() a,
a,
由射影定理可得![]() ,∴
,∴![]() ,
,
解得:a=![]() (负值已舍),∴
(负值已舍),∴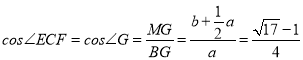 .
.
(3)如图2,连接DE,延长DG、AC相交于H,
由射影定理知![]() .
.
∵AC=BC,CD⊥AB,
∴AD=BD,
∴DE∥AH,
∴DE=![]() AC,
AC,![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴DE=![]() CH,
CH,
![]() ,
,
![]() ,
,
![]() ,
,
∴EG=![]() GC,
GC,
∴GC=2,
![]() EC=3=BE=DE,
EC=3=BE=DE,
在![]() 中,根据勾股定理得DG=
中,根据勾股定理得DG=![]() ,
,
∴DG=![]() .
.
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案