Question

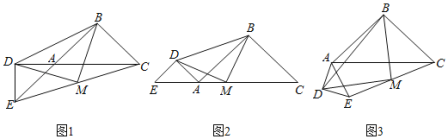
【题目】如图，已知AF=AB，∠FAB=60°，AE=AC，∠EAC=60°，CF和BE交于O点，则下列结论：①CF=BE；②∠COB=120°；③OA平分∠FOE；④OF=OA+OB．其中正确的有_____．

Answer 1

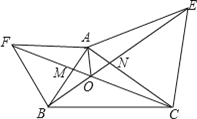
【答案】①②③④．

【解析】

结合等边三角形△ABF和△ACE的性质，利用SAS可证△ABE≌△AFC，由全等三角形的性质可知①正确；由三角形内角和为180度易求∠BOC的度数，可知②正确；连接AO，过A分别作AP⊥CF与P，AM⊥BE于Q，由S△ABE=S△AFC可知AP=AQ，利用HL定理可证，易知OA平分∠FOE，所以③正确；在OF上截取OD=OB，利用SAS可证△FBD≌△ABO，由全等三角形对应边相等易得OF= OA+OB，故④正确.

解：∵△ABF和△ACE是等边三角形，

∴AB=AF，AC=AE，∠FAB=∠EAC=60°，

∴∠FAB+∠BAC=∠EAC+∠BAC，即∠FAC=∠BAE，

在△ABE与△AFC中，

，

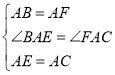∴△ABE≌△AFC(SAS)，

∴BE=FC，∠AEB=∠ACF，故①正确；

∵∠EAN+∠ANE+∠AEB=180°，∠CON+∠CNO+∠ACF=180°，∠ANE=∠CNO，∴∠CON=∠CAE=60°=∠MOB，

∴∠BOC=180°﹣∠CON=120°，故②正确；

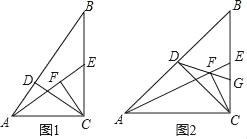
连接AO，过A分别作AP⊥CF与P，AM⊥BE于Q，如图1，

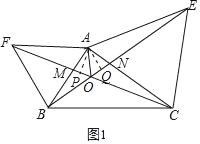
∵△ABE≌△AFC，∴S△ABE=S△AFC，∴CFAP=BEAQ，∵CF=BE，∴AP=AQ，

，∴OA平分∠FOE，所以③正确；

如图2，在OF上截取OD=OB，

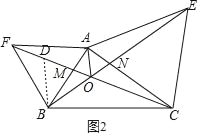
∵∠BOF=60°，∴△OBD是等边三角形，∴BD=BO，∠DBO=60°，∴∠FBD=∠ABO．

∵BF=AB，∴△FBD≌△ABO(SAS)，∴DF=OA，∴OF=DF+OD=OA+OB，故④正确．

故答案为：①②③④．