题目内容
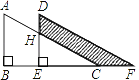
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”，如图（1），
，
，
，但
与
却不全等.但是如果两个直角三角形呢？如图（2）
，
，
,则
吗？
（1）根据图（2）完成以下证明和阅读：
和
中，
，
____________（勾股定理）
，
____________
，.
____________
在与中，
，，
____________（____________）
归纳：斜边和一条直角边相等的两个直角三角形全等；简称为“斜边直角边”或“
”.
几何语言如下：
在与中，
，
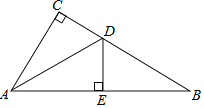
（2）如图（3）已知
，
；求证：
平分
.（每一步都要填写理由）
【答案】（1）详见解析；（2）详见解析.
【解析】
（1）根据勾股定理得到BC=EF,根据SSS证三角形全等；（2）根据HL证三角形全等，根据全等三角形性质得到∠ACB=∠ACD.
证明：（1）
和
中，
，
DE2（勾股定理）
，
DE2-DF2
，
.
EF
在
与
中，
，
，
（SSS）
（2）因为
（已知）
所以ABC和ADC是直角三角形（直角三角形定义）
因为AC=AC,
（已知）
所以ABC
ADC（HL）
所以∠ACB=∠ACD（全等三角形性质）
所以
平分
（角平分线定义）
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
