Question

【题目】正方形的边长为，点分别是线段上的动点，连接并延长，交边于，过作，垂足为，交边于点.

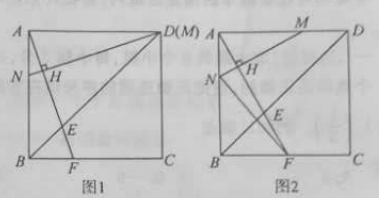
（1）如图1，若点与点重合，求证：；

（2）如图2，若点从点出发，以的速度沿向点运动，同时点从点出发，以的速度沿向点运动，运动时间为.

①设,求关于t的函数表达式；

②当时，连接，求的长.

Answer 1

【答案】（1）详见解析；（2）①；②5.

【解析】

试题分析：（1）根据已知条件易证△ABF≌△NAD，由全等三角形的性质即可得；（2）

先证△ABF∽△NAD，根据全等三角形的性质求得；（3）利用△ABF∽△NAD，求得t=2，根据（2）的函数解析式求得BF的长，再由勾股定理即可得FN的长.

试题解析：

【解】

（1）∵正方形

∴AD=AB,∠DAN=∠FBA=90°

∵

∴∠NAH+∠ANH=90°

∵∠NDA+∠ANH=90°

∴∠NAH=∠NDA

∴△ABF≌△NAD

∴

（2）①∵正方形

∴AD∥BF

∴∠ADE=∠FBE

∵∠AED=∠BEF

∴△EBF∽△EAD

∴

∵正方形

∴AD=DC=CB=6

∴BD=

∵点从点出发，以的速度沿向点运动，运动时间为.

∴BE=，DE=

∴

∴

②当时，连接，求的长.

∵正方形

∴∠MAN=∠FBA=90°

∵

∴∠NAH+∠ANH=90°

∵∠NMA+∠ANH=90°

∴∠NAH=∠NMA

∴△ABF∽△NAD

∴

∵，AB=6

∴AN=2,BN=4

∴

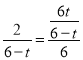
∴t=2

把t=2代入，得y=3，即BF=3,

在RT△BFN中，BF=3,BN=4,

根据勾股定理即可得FN=5.